10. Sınıf Matematik Ders Kitabı Sayfa 110 Cevapları Hecce Yayıncılık

ALIŞTIRMALAR

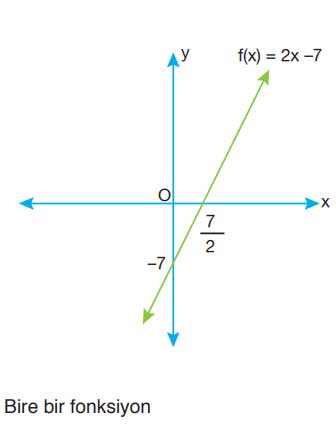
Soru 1- f : R → R, f(x) = 2x - 7 olmak üzere f fonksiyonunun grafiğini çizip bire bir olup olmadığını gösteriniz.

Cevap: Fonksiyonun bire bir olup olmadığını anlamak için f(x₁) = f(x₂) koşulunu inceleyelim:
f(x₁) = f(x₂) ⇒ 2x₁ - 7 = 2x₂ - 7 ⇒ x₁ = x₂
Bu durumda fonksiyon bire birdir. Fonksiyonun grafiği bir doğrudur ve eğimi m = 2, y-eksenini kestiği nokta -7’dir. Grafikten her x değeri için yalnızca bir y değeri olduğu görülür.

x = 0 için y = -7
y = 0 için x = 7/2

Sonuç: Çektiğimiz doğrular hep bir noktada kesiyor, o halde bire birdir.

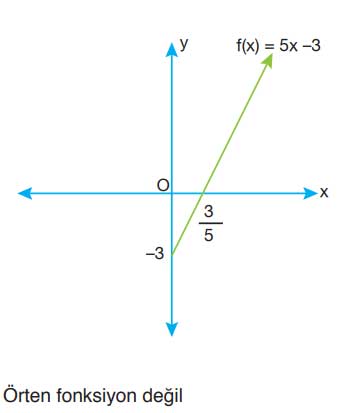
Soru 2 f : R⁺ → R, f(x) = 5x - 3 olmak üzere f fonksiyonunun grafiğini çizip örten olup olmadığını bulunuz.

Cevap: Fonksiyonun tanım kümesi R⁺ olduğu için negatif x değerleri alınamaz. Fonksiyonun değer kümesi R’yi tam olarak kapsamaması nedeniyle örten değildir. Grafikte y = 5x - 3 doğrusu çizilir ve sadece x > 0 bölgesinde tanımlıdır.

Çözüm:
x = 0 için y = -3
y = 0 için x = 3/5

Sonuç: Tanım kümesine negatif değer veremediğimizden tüm gerçek sayıları kapatamaz. Bu yüzden örten değildir.

Soru 3 f : R → R, f(x) = 4x + 5 olmak üzere f fonksiyonunun bire bir olup olmadığını cebirsel olarak gösteriniz.

Cevap: Fonksiyonun bire bir olup olmadığını anlamak için f(x₁) = f(x₂) denklemini çözelim:
f(x₁) = f(x₂) ⇒ 4x₁ + 5 = 4x₂ + 5 ⇒ x₁ = x₂
Bu işlem fonksiyonun bire bir olduğunu kanıtlar.

a, b ∈ R olacak şekilde a ve b değerleri alalım.
f(a) = 4a + 5, f(b) = 4b + 5 ise f(a) = f(b) olsun.
O halde 4a + 5 = 4b + 5, a = b olduğuna göre bire birdir.

Soru 4 f : R → R, f(x) = 3x² - 1 olmak üzere f fonksiyonunun bire bir olup olmadığını cebirsel olarak gösteriniz.

Cevap: Fonksiyonun bire bir olup olmadığını anlamak için f(x₁) = f(x₂) denklemini çözelim:
f(x₁) = f(x₂) ⇒ 3x₁² - 1 = 3x₂² - 1 ⇒ x₁² = x₂² ⇒ x₁ = ±x₂
Aynı y değeri için birden fazla x değeri olabildiği için fonksiyon bire bir değildir.

a, b ∈ R olacak şekilde a ve b alalım.
f(a) = 3a³ - 1, f(b) = 3b³ - 1 ise f(a) = f(b) olsun.
3a³ - 1 = 3b³ - 1 ⇒ a³ = b³ ⇒ a = b

Sonuç: Fonksiyon bire birdir.

Soru 5 Aşağıda tanım ve değer kümeleri ile grafikleri verilen fonksiyonların bire bir ve örten olup olmadıklarını inceleyiniz.

Cevap:

• a) Fonksiyon bire birdir, ancak değer kümesindeki tüm elemanları kapsamadığı için örten değildir.
• b) Fonksiyon bire bir değildir ve örten değildir.
• c) Fonksiyon bire bir değildir ve örten değildir.
• d) Fonksiyon bire birdir, ancak y = 0 değerini kapsamadığı için örten değildir.

a) f : R → R
Fonksiyonun grafiğinden görüldüğü üzere aynı y değerine farklı x değerleri karşılık geliyor. Bu nedenle bire bir değildir. Ancak grafiğin tüm değer kümesini kapsadığı için örtendir.
Sonuç: Bire bir değil, örtendir.

b) g : R → R
Fonksiyonun grafiğinden görüldüğü üzere aynı y değerine birden fazla x değeri karşılık geliyor ve değer kümesini de tam olarak kapsamıyor.
Sonuç: Bire bir değil, örten değildir.

c) h : R → R
Grafikten, aynı y değerine birden fazla x değeri karşılık geldiği ve değer kümesini tam olarak kapsamadığı görülür.
Sonuç: Bire bir değil, örten değildir.

d) s : R → R \ {0}
Fonksiyonun grafiğinden görüldüğü üzere her y değerine yalnızca bir x değeri karşılık geliyor. Ancak değer kümesinde 0 bulunmadığı için örtmez.
Sonuç: Bire birdir, örten değildir.

Soru 6 A = {-2, -1, 0, 1, 2}, B = {-8, -1, 0, 1, 8}, f : A → B, f(x) = x³ olmak üzere f fonksiyonunun bire bir ve örten olup olmadığını bulunuz.

Cevap: Fonksiyonun her x değeri farklı bir y değerine karşılık geldiğinden bire birdir. Ayrıca, A’nın her elemanının B’de bir karşılığı olduğu için fonksiyon örtendir.

Fonksiyonun değerleri:
f(-2) = -8
f(-1) = -1
f(0) = 0
f(1) = 1
f(2) = 8

Her x değeri farklı bir y değerine karşılık geldiğinden fonksiyon bire birdir. Ayrıca, A’nın tüm elemanları B’de bir karşılığa sahiptir.
Sonuç: Fonksiyon bire birdir ve örtendir.

Soru 7 f : R → R, f(x) = 3x + 8 olmak üzere f fonksiyonunun bire bir ve örten olup olmadığını bulunuz.

Cevap: Fonksiyon doğrusal olduğundan, her x için farklı bir y değeri vardır ve bu nedenle bire birdir. Ayrıca, her y değeri için bir x bulunduğundan örtendir.

Fonksiyon y = f(x) = 3x + 8
y = 3x + 8 eşitliğinden:

• x = 0 için y = 8
• y = 0 için x = -8/3

Grafikten görüldüğü üzere fonksiyon doğrusal bir fonksiyondur. Her x değeri için yalnızca bir y değeri bulunduğundan bire birdir ve her y değeri için bir x bulunduğundan örtendir.

Sonuç: Bire bir ve örtendir.

Soru 8 f : R → R, f(x) = 2^x olmak üzere f fonksiyonunun grafiğini çizerek örten olup olmadığını test ediniz.

Cevap: Fonksiyonun tanım kümesi R, değer kümesi (0, ∞)’dir. Her x için farklı bir y değeri bulunduğundan bire birdir, ancak değer kümesindeki negatif y değerlerini kapsamadığı için örten değildir.

Fonksiyon y = f(x) = 2x²

• x = 0 için y = 0
• x = 1 için y = 2
• x = 2 için y = 8
• x = -1 için y = 2
• x = -2 için y = 8

Grafikten görüldüğü gibi aynı y değeri için birden fazla x değeri bulunduğundan bire bir değildir. Ayrıca negatif y değerlerini almadığından örtmez.

Sonuç: Örten değildir, negatif değerleri almıyor.