10. Sınıf Matematik Ders Kitabı Sayfa 223 Cevapları Meb Yayınları

10. Sınıf Matematik – Alıştırmalar Sayfa 223 Soru Cevapları

1. Soru - a, b, c ve d katsayılarını küçükten büyüğe doğru sıralayınız.

Grafikten şunları görüyoruz:

• g(x) = −x² grafiği aşağı doğru açılan standart paraboldür. Bu, katsayısı −1 olan referans grafiktir.
• h(x) = a x² grafiği yukarı doğru açılıyor ve f(x)=x²’den daha geniş ise |a| < 1, daha dar ise |a| > 1’dir. Grafikten, h(x)’in f(x)’ten daha geniş olduğu görülüyor ⇒ 0 < a < 1.
• k(x) = b x² grafiği yukarı açılıyor ve f(x)=x²’den daha dar ⇒ b > 1.
• m(x) = c x² grafiği aşağı açılıyor fakat g(x)=−x²’den daha geniş ⇒ eğimi daha küçük mutlak değerde negatif ⇒ −1 < c < 0.
• t(x) = d x² grafiği aşağı açılıyor ve g(x) = −x²’den daha dar ⇒ mutlak değeri daha büyük negatif ⇒ d < −1.

O hâlde katsayıları küçükten büyüğe sıralarsak:

• En küçük: d (−1’den bile küçük, en negatif),
• Sonra: c (−1 ile 0 arasında),
• Sonra: a (0 ile 1 arasında),
• En büyük: b (1’den büyük).

Cevap: d < c < a < b

1. Soru (b) a, b, c ve d katsayılarının en geniş değer aralıklarını bulunuz.

a: Yukarı açılan paraboldür ve f(x) = x²’den daha geniş ⇒ 0 < a < 1
b: Yukarı açılan ve f(x)=x²’den daha dar ⇒ 1 < b < ∞
c: Aşağı açılan, g(x)=−x²’den daha geniş ⇒ −1 < c < 0
d: Aşağı açılan, g(x)=−x²’den daha dar ⇒ −∞ < d < −1

Cevap: 0 < a < 1, 1 < b < ∞, −1 < c < 0, −∞ < d < −1

2. Soru (a) Füzenin aldığı yolun zamana bağlı grafik gösterimini çiziniz.

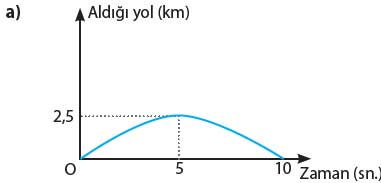
Cevap: Grafik aşağı doğru açılan bir parabol şeklindedir. Başlangıç noktası (0, 0), en yüksek noktası (5, 2,5) ve yere düştüğü nokta (10, 0)’dır.

Grafiğin özellikleri

• Parabol aşağı açılır
• Tepe noktası: (5, 2,5)
• Yerden atıldığı an: t = 0
• Yere düştüğü an: t = 10

Grafik: (0,0) → (5,2,5) → (10,0)

2. Soru (b) Roketin yerden çıkabildiği en yüksek mesafeyi bulunuz.

Maksimum yükseklik, tepe noktasının y değeridir.
Tepe noktası (5, 2,5) olduğuna göre:
Maksimum yükseklik = 2,5 km

Cevap: Roketin ulaştığı en büyük yükseklik 2,5 km’dir.

2. Soru (c) Roket, atıldıktan kaç saniye sonra yere düşmüştür?

Roketin yere düşmesi demek, yüksekliğin 0 olması demektir: f(t) = 0.

(t − 5)² = 25
t = 0 veya t = 10

t = 0 atış anıdır, bu yüzden yere düşme anı:

Roket 10 saniye sonra yere düşer.

3. Soru (a) Firmanın kârının maksimum olması için kaç adet üretim yapması gerekir?

Cevap: Firmanın maksimum kâr elde edebilmesi için 10 adet üretim yapması gerekir.

Kâr = Gelir − Maliyet

k(x) = g(x) − m(x)
k(x) = (−2x² + 50x) − (10x + 100)
k(x) = −2x² + 50x − 10x − 100
k(x) = −2x² + 40x − 100

Bu yine aşağı açılan bir parabol (a = −2).

Bir parabolda maksimum (veya minimum) değeri veren x,
xₜ = −b / (2a) formülü ile bulunur.
Burada k(x) = −2x² + 40x − 100 → a = −2, b = 40.

xₜ = −b / (2a)
xₜ = −40 / (2·(−2))
xₜ = −40 / (−4)
xₜ = 10

Maksimum kâr için x = 10 adet üretim yapılmalıdır.

3. Soru (b) Firmanın elde edeceği maksimum kâr kaç TL’dir?

Cevap: Firmanın elde edeceği maksimum kâr 100 TL’dir.

x = 10’u k(x)’te yerine yazalım:

k(10) = −2·(10)² + 40·10 − 100
k(10) = −2·100 + 400 − 100
k(10) = −200 + 400 − 100
k(10) = 100

Firmanın elde edeceği maksimum kâr 100 TL’dir.

4. Soru (a) Arsanın bir kenar uzunluğuna bağlı alan fonksiyonunu yazınız.

Cevap: a(x) = 200x − x²

Dikdörtgende çevre:

2x + 2y = 400
x + y = 200
y = 200 − x

Alan: A = x·y

A(x) = x · (200 − x)
A(x) = 200x − x²

Alan fonksiyonu: A(x) = 200x − x²

4. Soru (b) Arsanın alanının maksimum olması için kenar uzunlukları kaç metre olmalıdır?

Cevap: Arsanın alanının en büyük olması için kenar uzunlukları 100 m ve 100 m olmalıdır.

A(x) = 200x − x²
Burada a = −1, b = 200 (yani A(x) = −x² + 200x).

Yine parabolün tepe noktasını bulalım:

xₜ = −b / (2a)
xₜ = −200 / (2·(−1))
xₜ = −200 / −2
xₜ = 100

Bu x değeri, alanın maksimum olduğu uzunluktur.

Diğer kenar için:
y = 200 − x = 200 − 100 = 100

Kenarlar 100 m ve 100 m olmalıdır.
Yani maksimum alan bir kare ile elde edilir.

4. Soru (c) Arsanın alabileceği en büyük alan kaç metrekaredir?

Cevap: Arsanın alabileceği maksimum alan 10 000 m²’dir.

A(100) = 200·100 − 100²
A(100) = 20 000 − 10 000
A(100) = 10 000

Maksimum alan = 10 000 m²

4. Soru (ç) Alan fonksiyonunun grafik gösterimini çiziniz.

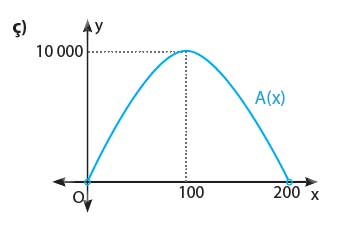
Cevap: Grafik, tepe noktası (100, 10 000) olan aşağı doğru açılmış bir paraboldür.
Fonksiyonun x eksenini kestiği noktalar x = 0 ve x = 200’dür.

A(x) = 200x − x²

• a = −1 → parabol aşağı açılır
• x–ekseniyle kesişim noktaları için A(x) = 0:

200x − x² = 0
x(200 − x) = 0
x = 0 veya x = 200

Yani:

• x = 0 iken alan = 0
• x = 200 iken alan = 0
• x = 100 iken alan maksimum = 10 000

Grafik; (0, 0)’dan başlar, (100, 10 000)’de tepe yapar, (200, 0)’da tekrar sıfıra iner. Aşağı açılan bir paraboldür.