10. Sınıf Matematik Ders Kitabı Sayfa 72 Cevapları Meb Yayınları

Alıştırmalar 1.7

1. Soru: Süreç içerisinde Ferhat'ın soruyu çözmesiyle durdurduğu zamanın virgülden sonraki kısmına ait bir sayı seçiliyor. Bu sayının: a) 8'e bölünebilme olasılığı nedir?
b) 50'den büyük olma olasılığı nedir?
c) Çift sayı olma olasılığı nedir?

Çözüm:

• a) 00'dan 99'a kadar olan sayılarda, 8'e bölünebilen sayılar: 00, 08, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96. Toplamda 13 sayı vardır. Olasılık: 13/100.
• b) 50'den büyük sayılar 51-99 arasıdır. Toplamda 49 sayı vardır. Olasılık: 49/100.
• c) Çift sayılar 00, 02, 04, ... 98 arasında sıralanır ve toplamda 50 tane çift sayı vardır. Olasılık: 50/100 = 1/2.

2. Soru: İki zar birlikte atıldığında zarların toplamının asal sayı olma olasılığı nedir?

Çözüm: Zarların toplamı 2'den 12'ye kadar değerler alabilir. Asal sayılar: 2, 3, 5, 7, 11. Olası asal toplamlar şu kombinasyonlarla elde edilir: (1,1), (1,2), (1,4), (1,6), (2,3), (2,5), vb. Toplamda 15 olası kombinasyon vardır. Olasılık: 15/36 = 5/12.

3. Soru: Bir torbadan rastgele bir topun kırmızı olma olasılığı 1/2'dir. Buna göre rastgele alınan 2 topun da kırmızı olma olasılığını bulun.

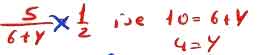
4. Soru: Bir çark üzerinde 1 numaralı parçaya ait göstergenin gelme olasılığını bulun.

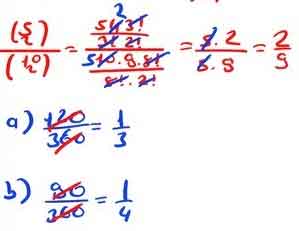
5. Soru: 7 madeni paranın atılması deneyinde en az 5 tanesinin tura gelme olasılığını bulun.

Çözüm: 7 madeni paranın aynı anda havaya atılması deneyinde en az 5 tanesinin tura gelme olasılığı şu şekilde hesaplanır:

7 madeni paranın atılmasıyla toplam 128 farklı olasılık vardır (2^7). En az 5 tura gelmesi durumları şunlardır: 5, 6 veya 7 tura gelme durumu.

Bu durumlar için hesaplamalar yapılır:

• 7 paradan 5'inin tura gelmesi olasılığı: C(7,5) = 21
• 7 paradan 6'sının tura gelmesi olasılığı: C(7,6) = 7
• 7 paranın hepsinin tura gelmesi olasılığı: C(7,7) = 1

Toplam uygun durum sayısı: 21 (5 tura) + 7 (6 tura) + 1 (7 tura) = 29

Bu durumda, toplam olasılık: P(en az 5 tura) = 29/128

6. Soru: (x – y)⁴ ifadesinin açılımındaki terimlerden rastgele biri seçildiğinde bu terimin katsayısının negatif veya 1 olma olasılığını bulun.

Çözüm: (x - y)⁴ ifadesinin açılımındaki terimlerden rastgele biri seçildiğinde bu terimin katsayısının negatif veya 1 olma olasılığı şu şekildedir:

Bu binom açılımında toplamda 5 terim vardır. Terimlerden birinin katsayısının negatif olma durumu veya 1 olma durumu şu şekilde hesaplanır:

Açılımda x ve y terimlerinin üslerine göre katsayısı negatif veya 1 olabilecek terimlerin olasılığı hesaplanır. Birinci ve sonuncu terimlerde katsayılar pozitif olacaktır. Orta terimlerde ise negatif olma olasılığı vardır. Bu terimlerden ikisinin katsayısı negatif, bir terimin katsayısı ise 1 olacaktır.

Toplamda 3 uygun terim vardır. 5 terim olduğu için: P(katsayı negatif veya 1) = 3/5

7. Soru: 4'ü doğrusal 8 farklı noktadan rastgele seçilen 3 noktanın bir üçgenin köşeleri olma olasılığını bulun.

Çözüm: 4'ü doğrusal 8 farklı noktadan rastgele seçilen 3 noktanın bir üçgenin köşeleri olma olasılığı şu şekildedir:
8 noktadan 3 nokta seçmenin toplam olasılığı 56'dır. 4 doğrusal noktadan 3'ünü seçmenin olasılığı ise 4'tür.
Doğrusal olan noktalar üçgen oluşturmaz, bu yüzden doğrusal noktaların seçilmesini toplamdan çıkarıyoruz:
(56 - 4) / 56 = 52 / 56 = 13 / 14
Sonuç olarak, üçgen oluşturma olasılığı 13/14'tür.

8. Soru: Otelde yan yana veya farklı katlarda kalma olasılıklarını hesaplayın.

Çözüm:

a) Yan yana odalarda kalma olasılığı:
Her katta 2 yan yana oda çifti vardır ve toplamda 3 kat olduğu için toplamda 6 yan yana oda çifti vardır. 9 odadan herhangi 2 oda seçmenin olasılığı 36'dır.
Yan yana odalarda kalma olasılığı 6/36 = 1/6'dır.

b) Farklı katlardaki odalarda kalma olasılığı:
Hatice ve Fatma'nın farklı katlarda kalma olasılığı, 6/8 = 3/4'tür.

c) Yan yana odalarda kalmama olasılığı:
Yan yana odalarda kalmama olasılığı, 1 - 1/6 = 5/6'dır.