10. Sınıf Matematik Ders Kitabı Sayfa 84-85 Cevapları Hecce Yayıncılık

ALIŞTIRMALAR

1. Soru 1. A = {–2, –1, 0, 1, 2}, B = {–3, –2, –1, 0, 1, 2}, f: A → B, f(x) = x² – 3 veriliyor. f eşleştirmesi için aşağıdaki ifadelerin başında yer alan yay ayraca, ifadeler doğruysa “D”, yanlışsa “Y” yazınız.

Verilen bilgiler:

• A = {-2, -1, 0, 1, 2}
• B = {-3, -2, -1, 0, 1, 2}
• f: A → B, f(x) = x² - 3

Bu bilgilere göre ifadeleri değerlendirelim:

a) f eşleşmesi bir fonksiyondur. (D)

b) f ‘nin tanım kümesi A, görüntü kümesi f(B) olur. (D)

c) f bire bir fonksiyondur. (Y)
Fonksiyon bire bir değil çünkü aynı görüntüyü farklı elemanlardan alabilir.

d) f içine fonksiyondur. (D)

e) f örten fonksiyondur. (Y)
Örten değil çünkü B’deki tüm elemanları kapsamaz.

f) f fonksiyonu çift fonksiyondur. (Y)
Çift fonksiyon değil çünkü f(x) = x³ - 3, tek dereceli bir fonksiyondur ve simetrik değildir.

2. Soru- Aşağıda boş bırakılan yerleri uygun ifadelerle tamamlayınız.

a) A → B, her x₁, x₂ ∈ A için f(x₁) ≠ f(x₂) iken x₁ ≠ x₂ ise f fonksiyonu bire bir olur.

b) Tanım kümesinin alt aralıklarında farklı kurallarla verilen fonksiyona parçalı fonksiyon denir.

c) f: A → B, f fonksiyonu verilmiş. f(A) ≠ B ise f fonksiyonu içine fonksiyon olur.

d) f: A → B, f fonksiyonu verilmiş. f(A) = B ise f fonksiyonu örten olur.

3. Soru - Bir tekstil atölyesinde 8 saatlik çalışma süresine 80 TL gündelik veriliyor. Fazladan çalışma yapıldığında 1 saat karşılığında, günlük saat ücretinin %50 fazlası ödeniyor. Ayrıca toplam fazla çalışma ücretine 5 TL ekleniyor.

• Fazla çalışma saati x ve buna göre alınan ücret f(x) olsun.
• Günlük saat ücreti = 80 TL / 8 saat = 10 TL/saat
• Fazladan çalışma ücreti = 10 TL * 1.5 = 15 TL

Fonksiyon: f(x) = 15x + 5

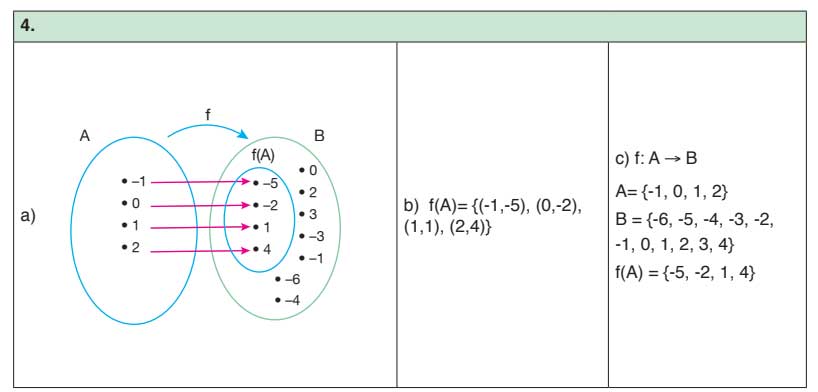
4. Soru: A = {-1, 0, 1, 2}, B = {-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4}, f: A → B ve f(x) = 3x - 2 olmak üzere f fonksiyonunu

a) Venn şeması ile gösteriniz.
Cevap: Venn şeması çizilir.

b) Liste yöntemi ile gösteriniz.
Cevap: f(-1) = -5, f(0) = -2, f(1) = 1, f(2) = 4
Liste: {(-1, -5), (0, -2), (1, 1), (2, 4)}

c) f fonksiyonunun tanım, değer ve görüntü kümelerini bulunuz.
Cevap:
Tanım kümesi = A
Değer kümesi = B
Görüntü kümesi = {-5, -2, 1, 4}

5. Soru: f: R → R, f(x) = { x² + 3, x ≤ 5; 2x - 7, x > 5 }

olduğuna göre f(4) kaça eşittir? f(6) kaça eşittir?

Cevap:
f(6) = 2 * 6 - 7 = 12 - 7 = 5
f(4) = 4² + 3 = 16 + 3 = 19
f(6) + f(4) = 5 + 19 = 24

Cevap: 24

6. Soru - f: R → R, f(x) = ax - 4 olmak üzere f fonksiyonu veriliyor. f(3) = 14 olduğuna göre f(a) değerini bulunuz.

Cevap:
f(3) = a * 3 - 4 = 14
3a - 4 = 14
3a = 18
a = 6
f(a) = f(6) = 6 * 6 - 4 = 36 - 4 = 32
Cevap: f(a) = 32

7. Soru - f: R → R, f(x) = x² + 3x - 5 olmak üzere f fonksiyonu veriliyor. f(-2) + f(1) işleminin sonucunu bulunuz.

Cevap:

f(-2) = (-2)² + 3 * (-2) - 5 = 4 - 6 - 5 = -7
f(0) = 0² + 3 * 0 - 5 = 0 - 5 = -5
f(1) = 1² + 3 * 1 - 5 = 1 + 3 - 5 = -1
f(-2) + f(0) - f(1) = -7 + (-5) - (-1) = -7 - 5 + 1 = -11

Cevap: -11

8. Soru: Yanda verilen fonksiyon makinesine göre

a) f(1)
b) f(-3)
c) f(2x)
d) f(3x - 3)

ifadelerinin değerlerini bulunuz.

Cevap: Fonksiyon makinesi f(x) = 6x - 5 olarak verilmiştir.

Çözümler:

a) f(1) = 6 * 1 - 5 = 6 - 5 = 1
b) f(-3) = 6 * (-3) - 5 = -18 - 5 = -23
c) f(x + 1) = 6 * (x + 1) - 5 = 6x + 6 - 5 = 6x + 1
ç) f(2x) = 6 * (2x) - 5 = 12x - 5
d) f(3x - 3) = 6 * (3x - 3) - 5 = 18x - 18 - 5 = 18x - 23

Sonuçlar:

• a) f(1) = 1
• b) f(-3) = -23
• c) f(x + 1) = 6x + 1
• ç) f(2x) = 12x - 5
• d) f(3x - 3) = 18x - 23

9. Soru: f: R → R, f(x + 1) = 8x - 13 olduğuna göre f(7) değerini bulunuz.

Cevap:

f(6x + 1) = 8x - 13 olduğuna göre, f(7) ifadesini bulmak için 6x + 1 = 7 olacak şekilde x değerini belirleyelim.

6x + 1 = 7 denklemini çözelim:

6x = 6
x = 1

Şimdi x = 1 değerini verilen ifadede yerine koyalım:

f(7) = 8 * 1 - 13
f(7) = 8 - 13
f(7) = -5

Cevap: -5

10. Soru

Soru: f: R → R, f(x) = (3a - 20)x + 2b + 6 şeklinde tanımlı f fonksiyonu birim fonksiyon olduğuna göre a + b değerini bulunuz.

Cevap:
Bir fonksiyonun birim fonksiyon olması için f(x) = x şeklinde olmalıdır.

Bu durumda:
3a - 20 = 1 ve 2b + 6 = 0 olmalıdır.
3a = 21 → a = 7
2b = -6 → b = -3
a + b = 7 - 3 = 4

11. Soru

Soru: f: R → R, f(x) = (a - 2)x² + (a + b - 5)x + 3a + b şeklinde tanımlı f fonksiyonu sabit fonksiyon olduğuna göre f(1) + f(2) + ... + f(10) değerini bulunuz.

Cevap:
Sabit fonksiyon olması için x'li terimlerin katsayıları 0 olmalıdır.

Bu durumda:
a - 2 = 0 → a = 2
a + b - 5 = 0 → b = 3

Fonksiyon sabit değer alır, bu değer:
f(x) = 3a + b = 3 * 2 + 3 = 6 + 3 = 9

f(1) + f(2) + ... + f(10) = 10 * 9 = 90

12. Soru

Soru: f: R - {4} → R, f(x) = (3x + a) / (x + 4) olmak üzere f fonksiyonu sabit fonksiyon olduğuna göre a değerini bulunuz.

Çözüm:
Bir fonksiyonun sabit olması için paydaki x terimlerinin katsayılarının sıfır olması gerekir. Yani, 3x + a ifadesinde x’li terimler birbirini sadelemeli.

Bu durumda, pay ve payda arasında aynı terimler olmalı. Bunu sağlamak için 3(x + 4) = 3x + a yazabiliriz, buradan a = 12 bulunur.

Cevap: a = 12

13. Soru

Soru: f(x) = (a - 1)x^2 + (b + 4)x şeklinde tanımlı f fonksiyonu birim fonksiyon, g(x) = (c - 5)x + 4 olmak üzere g fonksiyonu sabit fonksiyon ve h(x) = ax^2 + bx + c olduğuna göre h(5) değerini bulunuz.

Çözüm:
f birim fonksiyon olduğuna göre f(x) = x şeklinde olmalıdır. Buna göre katsayıları eşitleyelim:

1. a - 1 = 0 olduğundan a = 1.
2. b + 4 = 1 olduğundan b = -3.

g fonksiyonunun sabit olması için x’in katsayısının sıfır olması gerekir:

3. c - 5 = 0 olduğundan c = 5.

Bunları kullanarak h(x) fonksiyonunu yerine koyalım:

h(x) = x² - 3x + 5

Şimdi h(5) değerini bulalım:

h(5) = 5² - 3 * 5 + 5 = 25 - 15 + 5 = 15

Cevap: h(5) = 15

14. Soru

Soru: f: R → R ve f doğrusal fonksiyondur. f(-1) = -8, f(2) = 10 olduğuna göre f(4) değerini bulunuz.

Çözüm:
Doğrusal fonksiyon f(x) = ax + b şeklindedir.

1. f(-1) = -8 olduğuna göre: -a + b = -8

2. f(2) = 10 olduğuna göre: 2a + b = 10

Bu iki denklemi çözelim:

• İlk denklem: -a + b = -8
• İkinci denklem: 2a + b = 10

Birinci denklemi ikinci denklemden çıkarırsak:

3a = 18
a = 6

Bu değeri birinci denkleme yerleştirirsek:

-6 + b = -8
b = -2

Fonksiyon f(x) = 6x - 2 olur.

Şimdi f(4) değerini bulalım:

f(4) = 6 * 4 - 2 = 24 - 2 = 22

Cevap: f(4) = 22

15. Soru

Soru: f: R → R, f(x) = (x^2 - 3x + 4) / (x - 4) ve g: R → R, g(x) = x + 1 olduğuna göre f ve g fonksiyonlarının eşit olup olmadığını inceleyiniz.

Çözüm:
Fonksiyonları karşılaştırmak için f(x) fonksiyonunu sadeleştirelim. f(x) = (x^2 - 3x + 4) / (x - 4) ifadesini açarsak:

f(x) = ((x - 4)(x + 1)) / (x - 4)

Paydada ve payda aynı terimler olduğundan, x ≠ 4 şartıyla sadeleştirebiliriz:

f(x) = x + 1

Bu durumda f(x) ve g(x) fonksiyonları eşittir, ancak f(x) için x ≠ 4 koşulu geçerlidir. Yani f ve g fonksiyonları x = 4 hariç tüm reel sayılar için eşittir.

Cevap: f ve g fonksiyonları x = 4 hariç eşittir.

İşte tüm üslü ifadeleri sayı üstüne küçük yazarak soruların çözümlerini yeniden düzenliyorum:

16. Soru

Soru: A = {-1, 4}, B = {-2, -1, 4, 10, 14} olmak üzere f: A → B, f(x) = x² - 2 ve g: A → B, g(x) = 3x + 2 olduğuna göre f ile g fonksiyonlarının eşit olup olmadıklarını inceleyiniz.

Çözüm:
Fonksiyonların eşit olması için, A kümesindeki her x değeri için f(x) = g(x) olmalıdır.

A kümesindeki elemanlar için f(x) ve g(x) değerlerini hesaplayalım:

1. x = -1 için:

   • f(-1) = (-1)² - 2 = 1 - 2 = -1
   • g(-1) = 3(-1) + 2 = -3 + 2 = -1
   • f(-1) = g(-1)

2. x = 4 için:

   • f(4) = 4² - 2 = 16 - 2 = 14
   • g(4) = 3(4) + 2 = 12 + 2 = 14
   • f(4) = g(4)

Tüm elemanlar için f(x) = g(x) olduğundan, f ve g fonksiyonları eşittir.

Cevap: f ve g fonksiyonları eşittir.

17. Soru

Soru: Aşağıdaki fonksiyonların tek ya da çift fonksiyon olup olmadıklarını belirtiniz.

a) f(x) = -x² + 7
b) g(x) = x² - 5x
c) h(x) = x² + 3x + 5
ç) f(x) = x² + 9

Çözüm:
Bir fonksiyonun çift olması için f(-x) = f(x), tek olması için f(-x) = -f(x) olmalıdır.

a) f(x) = -x² + 7:

• f(-x) = -(x)² + 7 = -x² + 7 = f(x), yani çift fonksiyon.

b) g(x) = x² - 5x:

• g(-x) = (-x)² - 5(-x) = x² + 5x, yani ne tek ne de çift.

c) h(x) = x² + 3x + 5:

• h(-x) = (-x)² + 3(-x) + 5 = x² - 3x + 5, yani ne tek ne de çift.

ç) f(x) = x² + 9:

• f(-x) = (-x)² + 9 = x² + 9 = f(x), yani çift fonksiyon.

Cevap:
a) Çift fonksiyon
b) Ne tek ne çift
c) Ne tek ne çift
ç) Çift fonksiyon

18. Soru

Soru: f: R → R, f(x) = 3x + 6 ve g: R → R, g(x) = 3x + a fonksiyonları verilmiştir. (f + g)(-1) = 4 olduğuna göre a’nın değerini bulunuz.

Çözüm:
(f + g)(x) = f(x) + g(x) olarak tanımlıdır.

1. f(x) = 3x + 6 ve g(x) = 3x + a olduğuna göre: (f + g)(x) = (3x + 6) + (3x + a) = 6x + 6 + a

2. (f + g)(-1) = 4 olduğuna göre: 6(-1) + 6 + a = 4
   -6 + 6 + a = 4
   a = 4

Cevap: a = 4

19. Soru

Soru: f: R → R, f(x) = 3x - 5; g: R → R, g(x) = x² + 2 olmak üzere f ve g fonksiyonları için aşağıda verilenlerin değerlerini bulunuz.

a) (f + g)(2)
b) (f - g)(4)
c) (f · g)(-1)
ç) (f / g)(0)
d) (2f - 4g)(1)

Çözüm:
Fonksiyon değerlerini hesaplayalım:

a) (f + g)(2) = f(2) + g(2)
f(2) = 3 * 2 - 5 = 6 - 5 = 1
g(2) = 2² + 2 = 4 + 2 = 6
(f + g)(2) = 1 + 6 = 7

b) (f - g)(4) = f(4) - g(4)
f(4) = 3 * 4 - 5 = 12 - 5 = 7
g(4) = 4² + 2 = 16 + 2 = 18
(f - g)(4) = 7 - 18 = -11

c) (f · g)(-1) = f(-1) · g(-1)
f(-1) = 3 * (-1) - 5 = -3 - 5 = -8
g(-1) = (-1)² + 2 = 1 + 2 = 3
(f · g)(-1) = -8 * 3 = -24

ç) (f / g)(0) = f(0) / g(0)
f(0) = 3 * 0 - 5 = -5
g(0) = 0² + 2 = 2
(f / g)(0) = -5 / 2 = -5/2

d) (2f - 4g)(1) = 2f(1) - 4g(1)
f(1) = 3 * 1 - 5 = 3 - 5 = -2
g(1) = 1² + 2 = 1 + 2 = 3
(2f - 4g)(1) = 2 * (-2) - 4 * 3 = -4 - 12 = -16

Cevaplar:
a) 7
b) -11
c) -24
ç) -5/2
d) -16