10. Sınıf Matematik Ders Kitabı Sayfa 97-98 Cevapları Hecce Yayıncılık

ALIŞTIRMALAR

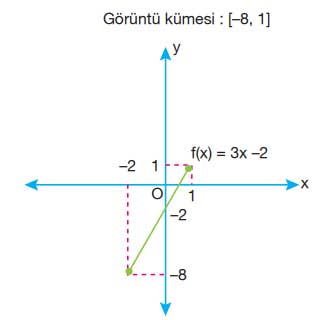
1. Soru: f: [-2, 1] → R, f(x) = 3x – 2 olmak üzere f fonksiyonu veriliyor. Buna göre f'nin görüntü kümesini bulup fonksiyonun bu aralıktaki grafiğini çiziniz.

Çözüm: f(x) = 3x - 2 fonksiyonu verilmiştir ve tanım aralığı [-2, 1]’dir. Bu aralıktaki en küçük ve en büyük x değerleri için f(x) değerlerini bulalım.

1. x = -2 için: f(-2) = 3(-2) - 2 = -6 - 2 = -8

2. x = 1 için: f(1) = 3(1) - 2 = 3 - 2 = 1

Bu durumda f'nin görüntü kümesi [-8, 1] aralığıdır.

Cevap: Görüntü kümesi [-8, 1].

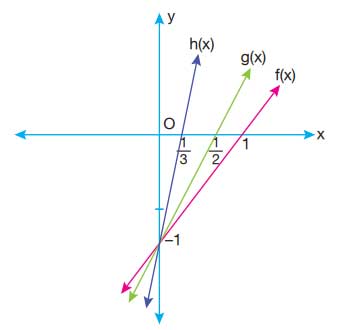
2. Soru: f: R → R, f(x) = x - 1, g: R → R, g(x) = 2x - 1 ve h: R → R, h(x) = 3x - 1 veriliyor. f, g ve h fonksiyonlarının grafiklerini çiziniz.

Çözüm: Bu fonksiyonlar doğrusal fonksiyonlardır ve hepsinin y eksenini kestiği nokta (0, -1)’dir. Eğimleri sırasıyla 1, 2 ve 3’tür. Bu yüzden grafiklerini çizmek için x ekseninde birkaç değer alarak y'yi bulabilirsiniz. Çizimde eğimi ve y eksenini kesme noktalarını kullanarak doğruyu oluşturabilirsiniz.

3. Soru: f: R → R,
f(x) =
x + 1, x < 0
2 - x, x ≥ 0
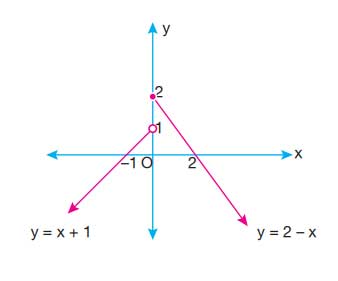
olmak üzere f fonksiyonunun grafiğini çiziniz.

Çözüm:
Bu parça parça tanımlı bir fonksiyondur. Grafiği çizmek için her aralık için f(x) fonksiyonunu çizin:

1. x < 0 için: f(x) = x + 1 (Bu doğrusal bir fonksiyon olup, y eksenini 1 noktasında keser ve eğimi 1'dir).
2. x ≥ 0 için: f(x) = 2 - x (Bu da doğrusal bir fonksiyon olup, y eksenini 2 noktasında keser ve eğimi -1'dir).

4. Soru: f: R → R,
f(x) =
3x - 1, x < -2
4x, -2 ≤ x < 4
-2x + 1, x ≥ 4
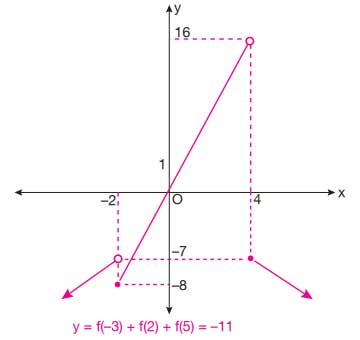
olmak üzere f fonksiyonunun grafiğini çizip f(-3) + f(2) + f(5) değerini bulunuz.

Çözüm: Her aralık için f(x) değerlerini bulup grafiği çiziniz:

1. x < -2 için: f(x) = 3x - 1

   • x = -3 için: f(-3) = 3(-3) - 1 = -9 - 1 = -10

2. -2 ≤ x < 4 için: f(x) = 4x

   • x = 2 için: f(2) = 4(2) = 8

3. x ≥ 4 için: f(x) = -2x + 1

   • x = 5 için: f(5) = -2(5) + 1 = -10 + 1 = -9

Toplam: f(-3) + f(2) + f(5) = -10 + 8 - 9 = -11

Cevap: f(-3) + f(2) + f(5) = -11

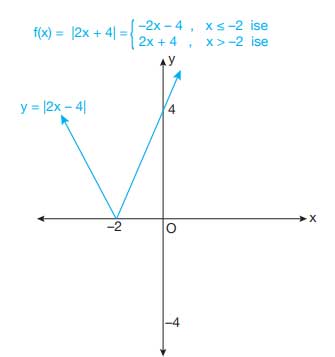
5. Soru: f: R → R, f(x) = |2x + 4| olmak üzere f fonksiyonunu parçalayıp grafiğini çiziniz.

Çözüm: Mutlak değer içindeki ifadeyi parçalayarak yazalım:

1. 2x + 4 ≥ 0 için (yani x ≥ -2): f(x) = 2x + 4

2. 2x + 4 < 0 için (yani x < -2): f(x) = -(2x + 4) = -2x - 4

Bu durumda f(x) fonksiyonunun parçalanmış hali:

f(x) =
2x + 4, x ≥ -2
-2x - 4, x < -2

Cevap:
Fonksiyonun parçalı hali:
f(x) =
2x + 4, x ≥ -2
-2x - 4, x < -2

6. Soru: Yanda grafiği verilen f fonksiyonunun tanım ve görüntü kümelerini bulunuz.

Çözüm: Grafikte f fonksiyonunun tanımlı olduğu x değerleri -7 ile 4 arasında değişmektedir. Bu nedenle:

Tanım Kümesi: −7,4-7, 4−7,4

Fonksiyonun y değerlerine bakıldığında ise en küçük değerin -3, en büyük değerin 4 olduğu görülmektedir. Bu nedenle:

Görüntü Kümesi: −3,4-3, 4−3,4

Cevap:
Tanım Kümesi: −7,4-7, 4−7,4
Görüntü Kümesi: −3,4-3, 4−3,4

7. Soru: Yanda grafiği verilen f fonksiyonunun tanım ve görüntü kümesini bulup
(f(-6) + f(-4) + f(-2)) / (f(0) + f(3) + f(6)) işleminin sonucunu hesaplayınız.

Çözüm: Grafiğe göre f fonksiyonunun tanım ve görüntü kümeleri:

• Tanım Kümesi: (-∞, 6]
• Görüntü Kümesi: (-∞, 6]

Fonksiyonun istenen değerlerini grafikten okuyarak bulalım:

1. f(-6) = 0
2. f(-4) = 3
3. f(-2) = 1
4. f(0) = 3
5. f(3) = 6
6. f(6) = 1

Bu değerlere göre işlemi yapalım:

(f(-6) + f(-4) + f(-2)) / (f(0) + f(3) + f(6)) = (0 + 3 + 1) / (3 + 6 + 1) = 4 / 10 = 1/2

Cevap:
Tanım Kümesi: (-∞, 6]
Görüntü Kümesi: (-∞, 6]
İşlemin Sonucu: 1/2

8. Soru: Yanda f fonksiyonunun grafiği verilmiştir. Buna göre fonksiyonun tanım ve görüntü kümesini bulup f(1) + f(2) + f(3) + f(0) değerini hesaplayınız.

Çözüm: Grafikten f fonksiyonunun tanım ve görüntü kümelerini belirleyebiliriz:

• Tanım Kümesi: (-∞, +∞)
• Görüntü Kümesi: (-∞, +∞)

Fonksiyonun istenen noktalarındaki değerlerini grafikten okuyalım:

1. f(1) = 5
2. f(2) = -1
3. f(3) = -1
4. f(0) = 7

Bu değerlere göre istenen toplam:

f(1) + f(2) + f(3) + f(0) = 5 + (-1) + (-1) + 7 = 10

Cevap:
Tanım Kümesi: (-∞, +∞)
Görüntü Kümesi: (-∞, +∞)
f(1) + f(2) + f(3) + f(0) = 10

9. Soru: Yanda f fonksiyonunun grafiği verilmiştir. Buna göre f(2x - 1) = 0 denklemini sağlayan x değerlerini bulunuz.

Çözüm: Grafikte f(x) = 0 olduğu noktalar x = -3, x = 2, ve x = 3’tür. Bu x değerlerini denklemdeki 2x - 1 ifadesine eşitleyerek bulalım:

1- f(2x - 1) = 0 ise 2x - 1 = -3

• 2x = -3 + 1
• 2x = -2
• x = -1

2- 2x - 1 = 3

• 2x = 3 + 1
• 2x = 4
• x = 2

3- 2x - 1

10. Soru: Yanda f fonksiyonunun grafiği verilmiştir. Buna göre A = [-7, -5], B = [-5, 0], C = [-1, 4] ve D = [5, 6] olmak üzere f(A), f(B), f(C) ve f(D) kümelerini bulunuz.

Çözüm: Grafikten her bir aralık için y değerlerini bulalım:

1. f(A) = f([-7, -5])

• Grafikte x değerleri -7 ile -5 arasında olduğunda y değerleri -3 ile 6 arasında değişmektedir.
• f(A) = [-3, 6]

2. f(B) = f([-5, 0])

• Grafikte x değerleri -5 ile 0 arasında olduğunda y değerleri -3 ile 5 arasında değişmektedir.
• f(B) = [-3, 5]

3. f(C) = f([-1, 4])

• Grafikte x değerleri -1 ile 4 arasında olduğunda y değerleri -1 ile 5 arasında değişmektedir.
• f(C) = [-1, 5]

4. f(D) = f([5, 6])

• Grafikte x değerleri 5 ile 6 arasında olduğunda y değerleri 0 ile 7 arasında değişmektedir.
• f(D) = [0, 7]

Cevap:
f(A) = [-3, 6]
f(B) = [-3, 5]
f(C) = [-1, 5]
f(D) = [0, 7]

11. Soru: Yanda f fonksiyonunun grafiği verilmiştir. Buna göre

a) Fonksiyonun tanım ve görüntü kümesini bulunuz.

b) (f(-2) + f(3)) / f(6) değerini hesaplayınız.

c) f(3a - 5) = 0 denklemini sağlayan a değerini bulunuz.

Çözüm:

a) Tanım ve Görüntü Kümesi

Grafikten f fonksiyonunun tanım ve görüntü kümeleri:

• Tanım Kümesi: [-4, 6]
• Görüntü Kümesi: [-3, 4]

b) (f(-2) + f(3)) / f(6) Değerini Hesaplayınız

Fonksiyonun grafiğinden istenen noktaların değerlerini okuyalım:

1. f(-2) = 0
2. f(3) = 3
3. f(6) = 1

İşlem:

(f(-2) + f(3)) / f(6) = (0 + 3) / 1 = 3

c) f(3a - 5) = 0 Denklemini Sağlayan a Değerini Bulunuz

Grafikte f(x) = 0 olduğu noktalar x = -2 ve x = 1’dir. Bu x değerlerini 3a - 5 ifadesine eşitleyerek a değerini bulalım:

1. 3a - 5 = -2

   • 3a = 3
   • a = 1

2. 3a - 5 = 1

   • 3a = 6
   • a = 2

Cevap:
a) Tanım Kümesi: [-4, 6], Görüntü Kümesi: [-3, 4]
b) (f(-2) + f(3)) / f(6) = 3
c) a = 1 veya a = 2