11. Sınıf Matematik Ders Kitabı Sayfa 75 Cevapları SDR Dikey Yayıncılık

Alıştırmalar 1-4

1. Aşağıdaki fonksiyonların periyotlarını bulunuz:

a) f(x) = 2sin(5x - 6)
Cevap: Sinüs fonksiyonunun periyodu 2π/5.

b) f(x) = 3sin(-2x + 4)
Cevap: Sinüs fonksiyonunun periyodu 2π/2 = π.

c) f(x) = -2cos(3x + 1)
Cevap: Kosinüs fonksiyonunun periyodu 2π/3.

ç) f(x) = -cot(x + 5)
Cevap: Kotanjant fonksiyonunun periyodu π.

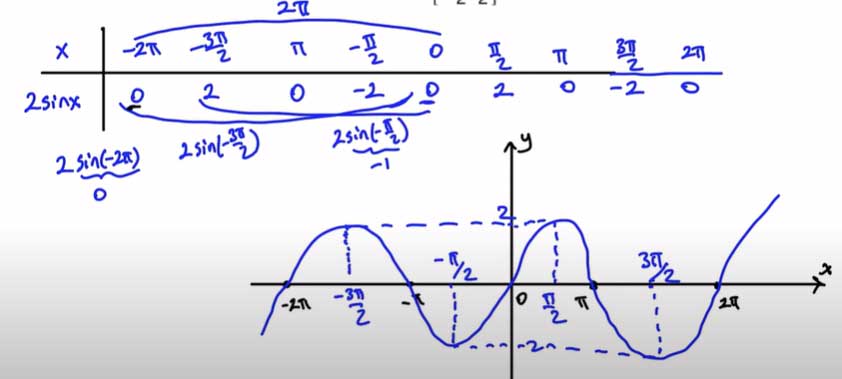
2. Aşağıdaki fonksiyonların grafiklerini bir dinamik matematik yazılımını kullanarak çiziniz.

Bu grafikler için, matematik yazılımlarında belirtilen aralıklarda grafikler çizilebilir:

• f(x) = 2sin x
• f(x) = cos x
• f(x) = -cot x
• f(x) = 2tan x

3. Aşağıda verilen ifadelerin değerlerini bulunuz:

a) arcsin(-1/2) + arccos(-1/2)
Cevap: arcsin(x) + arccos(x) = π/2. Bu yüzden değer π/2.

b) arctan(1/√3) + arctan(1)
Cevap: arctan(1/√3) = π/6 ve arctan(1) = π/4. Toplam:
π/6 + π/4 = 2π/12 + 3π/12 = 5π/12.

c) arctan 0 + arctan 1
Cevap: arctan(0) = 0, arctan(1) = π/4. Toplam: π/4.

4. tan(arccos(7/25)) ifadesinin değerini bulunuz.

arccos(7/25) üçgeni için: x = 7, hipotenüs: 25 → y = √(25² - 7²) = 24.
tan(θ) = karşı/komşu = 24/7.
Cevap: 24/7.

5. sin(arctan 1 + arccos 1/2 - arcsin 1/2) ifadesinin değerini bulunuz.

Verilen ifade: sin(arctan(1) + arccos(1/2) - 2 × arcsin(1/2))

Değerler:

• arctan(1) = 45° (veya π/4 radyan)
• arccos(1/2) = 60° (veya π/3 radyan)
• arcsin(1/2) = 30° (veya π/6 radyan)

Toplam ve fark:

• arctan(1) + arccos(1/2) - 2 × arcsin(1/2) = 45° + 60° - 2 × 30°
• = 45° + 60° - 60° = 45°

Sinüs hesaplaması:

• sin(45°) = √2 / 2.

İfadenin değeri: √2 / 2

6. arcsin(√3/2) + arccos(√3/2) = α ise, sin(α) nedir?

Verilen ifade: arcsin(√3/2) + arccos(√3/2) + arctan(√3) = α ve sin(α) değeri nedir?

Değerler:

• arcsin(√3/2) = 60° (veya π/3 radyan)
• arccos(√3/2) = 30° (veya π/6 radyan)
• arctan(√3) = 60° (veya π/3 radyan)

Toplam:

• arcsin(√3/2) + arccos(√3/2) + arctan(√3)
• = 60° + 30° + 60°
• = 150° (veya 5π/6 radyan)

Sinüs hesaplaması:

• sin(150°) = sin(180° - 30°) = sin(30°) = 1/2.

Cevap: sin(α) değeri: 1/2