9. Sınıf Fizik Ders Kitabı Sayfa 65-66-67 Cevapları Meb Yayınları

3. Etkinlik Vektörlerin Özellikleri

Bu etkinlik, vektörlerin özelliklerini incelemeye yönelik bir çalışmadır. Vektörlerin yönü ve büyüklüğü gibi temel özellikler, şekil üzerinde verilen örneklerle analiz edilir. Ayrıca, eşit vektörlerin tespit edilmesi ve yönlerin doğru bir şekilde belirlenmesi üzerinde durulmuştur.

Amaç: Öğrencilerin vektörlerin yön ve büyüklük özelliklerini doğru bir şekilde anlamalarını sağlamaktır.

Sonuç: Eşit vektörlerin, yön ve büyüklüklerine göre değerlendirilmesi yapılmıştır. Bu çalışmada vektörler Doğu ve Batı yönlerinde analiz edilerek büyüklükleri karşılaştırılmıştır.

Sayfa 65 Cevapları

a) Vektörlerin eşit bölmelendirilmiş düzlemde verilmesi, büyüklüklerinin belirlenmesi için bir kolaylıktır. Vektörlerin eşit bölmelendirilmiş bir düzlemde verilmediği durumda büyüklüklerini belirleyici özellikleri ne olabilir?

Cevap: Vektörlerin eşit bölmelendirilmiş bir düzlemde olmaması durumunda, büyüklüklerini belirlemek için uzunlukları ve yönleri kullanılabilir. Örneğin, vektörün başlangıç ve bitiş noktaları arasındaki mesafe büyüklüğün belirlenmesinde kullanılabilir.

b) Şekilde verilen vektörlerin yönlerini ve büyüklüklerini tablodaki ilgili bölümlere yazınız.

• A: Batı yönünde, 2 birim.
• B: Doğu yönünde, 4 birim.
• C: Batı yönünde, 2 birim.
• D: Doğu yönünde, 2 birim.
• E: Doğu yönünde, 4 birim.
• F: Doğu yönünde, 2 birim.

Bu değerlere göre, tablo doğru şekilde düzenlenmiştir. A ve C, D ve F vektörlerinin birbirine eşit olduğu görülmektedir, çünkü büyüklükleri ve yönleri aynıdır.

c) Şekildeki A ve C birbirine eşit vektörlerdir. Buna göre A ve C dışında başka hangi vektörler eşit vektörlerdir?

Cevap: B ve E, D ve F birbirine eşit vektörlerdir.

Sayfa 66 Cevapları

c) Şekildeki vektörlerden A ve D birbirine zıt vektörlerdir. Buna göre A ve D dışında başka hangi vektörler zıt vektörlerdir?

Cevap: A ve F, C ve F, D ve C zıt vektörlerdir.

Bu bilgiye göre, A ve F, C ve F, D ve C vektörlerinin yönleri zıt ve büyüklükleri eşittir, bu nedenle bu vektörler zıt vektörler olarak kabul edilir.

d) Şekildeki B ve D arasında B = 2D ilişkisi vardır. Buna göre B ve D dışında başka hangi vektörler arasında benzer bir ilişki vardır? Bir vektörün pozitif reel sayı ile çarpılması durumunda vektörün hangi özelliği değişir?

Cevap: B ve D vektörleri arasında B = 2D ilişkisi vardır. B ve D dışında, E ve F vektörleri arasında da benzer bir ilişki bulunmaktadır, yani E = 2F. Bu, büyüklük bakımından bir vektörün diğerinin iki katı olduğu anlamına gelir.

Bir vektörün pozitif reel sayı ile çarpılması durumunda, vektörün büyüklüğü değişir, ancak yönü değişmez. Pozitif reel sayılar yalnızca vektörün büyüklüğünü artırır veya azaltır, yönüne etki etmez.

e) Şekildeki vektörlerden B ve C arasında B = -2C ilişkisi vardır. Buna göre B ve C dışında başka hangi vektörler arasında benzer bir ilişki vardır? Bir vektörün negatif reel sayı ile çarpılması durumunda vektörün hangi özellikleri değişir?

Cevap: B ve C vektörleri arasında B = -2C ilişkisi vardır. Bu, B vektörünün büyüklüğünün C vektörünün iki katı, ancak yönlerinin zıt olduğu anlamına gelir. B ve C dışında, A ve E vektörleri arasında da benzer bir ilişki bulunmaktadır, yani E = -2A.

Bir vektörün negatif bir reel sayı ile çarpılması durumunda, vektörün yönü tersine döner, ancak büyüklüğü değişebilir. Negatif reel sayı, vektörün büyüklüğünü çarptığı sayı kadar artırır veya azaltır, fakat aynı zamanda yönünü değiştirir.

2. Vektörlerle ilgili aşağıda verilen soruları cevaplayınız.

a) İki vektörün eşit vektör olması için hangi özellikleri aynı olmalıdır?

Cevap: Eşit vektörler için büyüklükleri ve yönleri aynı olmalıdır.

b) İki vektörün zıt vektör olması için hangi özellikleri aynı olmamalıdır?

Cevap: Zıt vektörlerin yönleri zıt, büyüklükleri eşit olmalıdır.

c) Bir vektör reel sayı ile çarpılırsa vektörün hangi özellikleri değişebilir?

Cevap: Reel sayı ile çarpıldığında vektörün büyüklüğü değişir ve negatif bir sayı ile çarpıldığında yönü tersine döner.

3. Vektörlerin yön ve büyüklüklerine yönelik verdiğiniz cevapları arkadaşlarınızın cevaplarıyla karşılaştırınız. Topladığınız verileri analiz ederek eşit vektör, zıt vektör ve reel sayı ile çarpılmış vektör hakkındaki değerlendirmenizi yazarak arkadaşlarınızla paylaşınız.

Eşit vektörler, büyüklük ve yön bakımından aynıdır. Zıt vektörler, aynı büyüklüğe sahip olup yönleri ters olan vektörlerdir. Pozitif reel sayı ile çarpılan vektörün büyüklüğü değişir, yönü aynı kalır. Negatif reel sayı ile çarpılan vektörün ise hem büyüklüğü değişir hem de yönü tersine döner.

Sayfa 67 Değerlendirme Cevapları

Kenar uzunlukları 1 birim olan eşit bölmelendirilmiş düzlemler üzerinde aşağıda verilen işlemleri yapınız.

Soru 1: En az iki tane eşit vektör çiziniz.

Cevap: Eşit vektörler, aynı büyüklüğe ve aynı yöne sahip olan vektörlerdir. Örneğin, iki vektör 2 birim büyüklüğünde ve doğu yönünde olabilir. Bu vektörleri eşit kareli düzlemde çizmek, vektörlerin eşit olup olmadığını kolayca görmemizi sağlar.

Soru 2: Çizdiğiniz eşit vektörlerden biri için zıt vektör çiziniz.

Cevap: Zıt vektörler, aynı büyüklüğe sahip olup yönleri zıt olan vektörlerdir. Çizdiğimiz doğu yönündeki eşit vektörlerden birinin zıt vektörü, batı yönünde aynı büyüklüğe sahip olacaktır. Örneğin, 2 birim doğuya yönlendirilmiş bir vektörün zıt vektörü, 2 birim batıya yönlendirilmiş olacaktır.

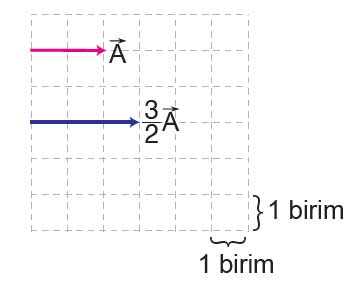
Soru 3: Büyüklüğü 2 birim olan bir vektör oluşturunuz ve bu vektörü 3/2 ile çarparak elde ettiğiniz vektörü çiziniz.

Cevap: Bir vektörü 3/2 ile çarpmak, vektörün büyüklüğünü arttırır. 2 birim büyüklüğündeki bir vektör 3/2 ile çarpıldığında, yeni vektörün büyüklüğü 3 birim olur. Yönü ise aynı kalır.

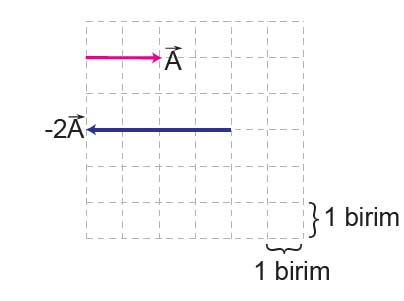
Soru 4: Büyüklüğü 2 birim olan bir vektör oluşturunuz ve bu vektörü -2 ile çarparak elde ettiğiniz vektörü çiziniz.

Cevap: Bir vektörü -2 ile çarpmak, hem büyüklüğünü değiştirir hem de yönünü tersine çevirir. 2 birimlik bir vektör -2 ile çarpıldığında, büyüklüğü 4 birim olur ve yönü tersine döner.

Soru 5: Eşit vektör, zıt vektör veya reel sayı ile çarpılmış vektörün günlük hayatta kullanıldığı bir örnek yazınız.

Cevap: Günlük hayatta rüzgarın etkisi altında bir uçağın hareketini düşünelim. Rüzgarın kuvveti ve yönü bir vektör olarak temsil edilebilir. Eğer rüzgar yön değiştirirse, uçağın hareketi zıt bir vektörel etki ile karşılaşır ve rotası buna göre ayarlanır. Benzer şekilde, rüzgarın şiddeti artarsa, vektör büyüklüğü değişir ve bu, uçağın hızını etkiler.