9. Sınıf Matematik 1. Ders Kitabı Sayfa 114-115 Cevapları Meb Yayınları

4. Sıra Sizde – Depodaki Buğday Miktarı (Sayfa 114–115)

a) f fonksiyonunun grafik temsilini inceleyiniz. Fonksiyon tek bir cebirsel gösterim ile ifade edilebilir mi? Açıklayınız.

Cevap: Hayır, f fonksiyonu tek bir cebirsel ifadeyle ifade edilemez. Çünkü grafik incelendiğinde üç farklı doğrusal parça görülmektedir.

• 0–3 gün arasında depodaki buğday miktarı sabittir (200 ton) ve eğim sıfırdır.

• 3–10 gün arasında her gün 100 ton buğday alınmıştır, grafik bu aralıkta pozitif eğimli bir doğru şeklindedir.

• 10–12 gün arasında alım hızı artmıştır, her gün 450 ton buğday alınmıştır.

Bu nedenle f fonksiyonu parçalı doğrusal fonksiyon şeklinde ifade edilir.

b) f fonksiyonunun grafik temsili yardımıyla gün başına depodaki buğday miktarını hesaplayınız.

Cevap: Grafikten her aralık için eğim (m) hesaplanarak günlük değişim miktarı bulunur:

• 0–3 gün aralığında: Depo sabit, eğim m = 0 ton/gün.

• 3–10 gün aralığında: 200 tondan 900 tona yükselmiştir.
  m = (900−200)/(10−3) = 100 ton/gün.

• 10–12 gün aralığında: 900 tondan 1800 tona yükselmiştir.
  m = (1800−900)/(12−10) = 450 ton/gün.

Sonuç olarak:

0–3 gün: 0 ton/gün
3–10 gün: 100 ton/gün
10–12 gün: 450 ton/gün

c) f fonksiyonunun cebirsel temsilini parçalı gösterimli fonksiyon biçiminde ifade ediniz. Grafik üzerinde gösteriniz.

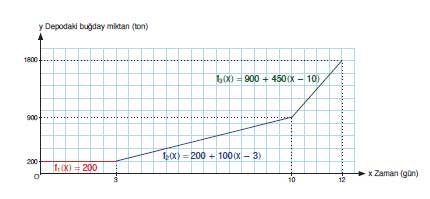
Bu fonksiyonun grafiğinde:

• 0–3 gün aralığında yatay bir doğru,
• 3–10 gün aralığında orta eğimli artan doğru,
• 10–12 gün aralığında ise daha dik artan bir doğru parçası bulunur.

Her parça, depodaki buğdayın farklı alım hızlarını temsil eder.

Genel Değerlendirme

Bu modelde depoda bulunan buğday miktarı zamana bağlı olarak parçalı doğrusal fonksiyon ile ifade edilir.
Her doğrusal parça, fabrikanın farklı dönemlerdeki alım hızını (ton/gün) gösterir.
12. günün sonunda hedeflenen 1800 ton miktarına ulaşılır.