9. Sınıf Matematik 1. Ders Kitabı Sayfa 131-132-133 Cevapları Meb Yayınları

Sayfa 132 9. Uygulama Cevapları
9. Uygulama
Gerçek Sayılarda g(x) = +- |ax + b| Şeklinde Tanımlı Mutlak Değer Fonksiyonlarının Cebirsel ve Grafiksel Temsili
Verilen bilgilere göre aşağıdaki soruları cevaplayınız.
Türkiye Cumhuriyeti Sağlık Bakanlığının verilerine göre sağlıklı bir bireyin vücut sıcaklığı için ortalama değer 36,5 oC olup vücut sıcaklığı, 35,7 oC ile 37,5 oC arasında değerler alabilmektedir.
1- Aşağıdaki tabloda sağlıklı bir bireyin gün boyunca farklı zamanlarda ölçülen vücut sıcaklığı değerleri ve ölçülen vücut sıcaklığı değerlerinin ortalamadan sapma miktarları verilmiştir.
a) Ölçülen vücut sıcaklığına bağlı ortalamadan sapma miktarının bağımlı ve bağımsız değişkenlerini sözel olarak ifade ediniz.
Bağımsız değişken, ölçülen vücut sıcaklığıdır.
Bağımlı değişken, bu sıcaklığın ortalamadan sapma miktarıdır.
b) Bağımlı ve bağımsız değişkenler hangi değerleri alabilir? Aralık şeklinde ifade ediniz.
Bağımlı değişken (Ortalamadan sapma miktarı):
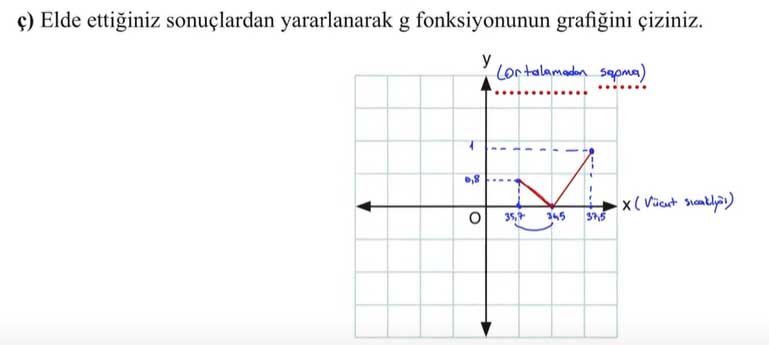
Bağımlı değişken, ölçülen vücut sıcaklığının ortalamadan sapma miktarını ifade eder. Bu değerler [0,8 , 1] aralığında değişir.
Bağımsız değişken (Ölçülen vücut sıcaklığı):
Bağımsız değişken, ölçülen vücut sıcaklığını ifade eder. Bu değerler [35,7 , 37,5] aralığında değişir.
c) Sağlıklı bir bireyin vücut sıcaklığına bağlı (x) ortalamadan sapma miktarını ifade eden g fonksiyonunun cebirsel temsili:
Cevap: g(x) = |x - 36.5|
ç) Elde ettiğiniz sonuçlardan yararlanarak g fonksiyonunun grafiğini çiziniz.
Cevap: Grafik, g(x) = |x - 36.5| fonksiyonunun grafiğidir. Simetrik bir V şekli oluşur.
d) g fonksiyonunun cebirsel temsili, parçalı gösterim şeklinde ifade edilebilir mi?
g(x) Fonksiyonu: g(x) = |x - 36,5|
Parçalı Gösterim Şeklinde İfade Edilmesi: g(x) fonksiyonu mutlak değer içerdiği için parçalı gösterimle şu şekilde ifade edilebilir:
-
Eğer x < 36,5 ise:
g(x) = -(x - 36,5)
g(x) = -x + 36,5 -
Eğer x ≥ 36,5 ise:
g(x) = x - 36,5
Sonuç: g(x) fonksiyonu parçalı gösterimle ifade edilebilir çünkü mutlak değer fonksiyonları, tanımlandığı bölgeye göre iki farklı cebirsel ifadeye sahiptir.
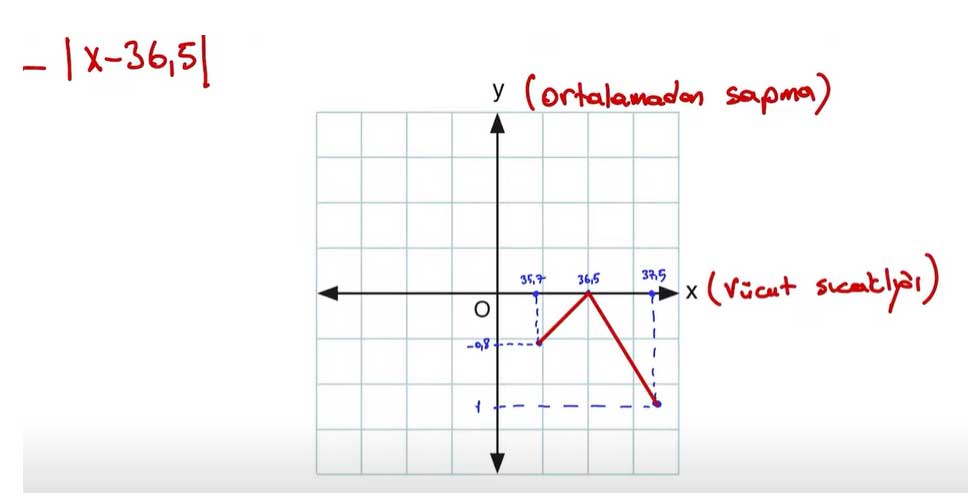
Soru 2 - g fonksiyonunun cebirsel temsilinin -1 ile çarpılmasıyla elde edilen fonksiyon h olsun. Gerçek sayılarda tanımlı h fonksiyonunun cebirsel temsilini yazarak grafiğini çiziniz.
g fonksiyonunun cebirsel temsili -1 ile çarpılmasıyla elde edilen h fonksiyonu:
Cevap:
h(x) = -( |x - 36.5| )
Bu fonksiyonun grafiği, g(x) grafiğinin x-eksenine göre yansımasıdır.
Sayfa 133 10. Uygulama Cevapları
1- a) f ve g fonksiyonlarının cebirsel ve grafiksel benzerliklerini, farklılıklarını gözlemleyiniz.
Cevap: Cebirsel olarak f(x) = |g(x)|. Grafiksel olarak:
- x < -b/a aralığında grafikler, x eksenine göre simetrik.
- x > -b/a aralığında grafikler aynıdır.
b) f ve h fonksiyonlarının cebirsel ve grafiksel benzerliklerini, farklılıklarını gözlemleyiniz.
Cevap: Cebirsel olarak f(x) = -|h(x)|. Grafiksel olarak:
- x < -b/a aralığında grafikler, x eksenine göre simetrik.
- x > -b/a aralığında grafikler aynıdır.
| Fonksiyonun Nitel Özellikleri | f(x) = ax + b | g(x) = |ax + b| | h(x) = -|ax + b| |
|---|---|---|---|
| En Geniş Tanım Kümesi | ℝ | ℝ | ℝ |
| Görüntü Kümesi | ℝ | [0, ∞) | (-∞, 0] |
| Fonksiyonun Sıfırı | -b/a | -b/a | -b/a |
| Fonksiyonun İşareti | (-∞, -b/a) → negatif, (-b/a, ∞) → pozitif | ℝ - {-b/a} → pozitif | ℝ - {-b/a} → negatif |
| Maksimum Nokta | Yok | 0 | Yok |
| Minimum Nokta | Yok | Yok | 0 |
| Bire Birliği | Bire bir | Bire bir değil | Bire bir değil |
| Artan veya Azalan Olduğu Aralıklar | Artan | (-∞, -b/a) → azalan, (-b/a, ∞) → artan | (-∞, -b/a) → artan, (-b/a, ∞) → azalan |
3. Elde ettiğiniz nitel özelliklerden yararlanarak g ve h mutlak değer fonksiyonlarının parçalı gösterimine dair çıkarımlarınızı açıklayınız.
Parçalı Gösterim Açıklaması:
g(x) fonksiyonu için parçalı gösterim:
g(x) =
-ax - b, x < -b/a
ax + b, x ≥ -b/a
h(x) fonksiyonu için parçalı gösterim:
h(x) =
ax + b, x < -b/a
-ax - b, x ≥ -b/a
Açıklama: Fonksiyonların parçalı gösterimi, mutlak değer içindeki ifadelerin, belirli bir sınır değerine (-b/a) göre iki farklı durumunu ifade eder:
- Birinci durum: x<−b/a olduğunda, mutlak değer içindeki ifade negatif alınır.
- İkinci durum: x≥−b/a olduğunda, mutlak değer içindeki ifade pozitif alınır.






Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.