9. Sınıf Matematik 1. Ders Kitabı Sayfa 143 Cevapları Meb Yayınları

Alıştırmalar Sorular ve Cevaplar
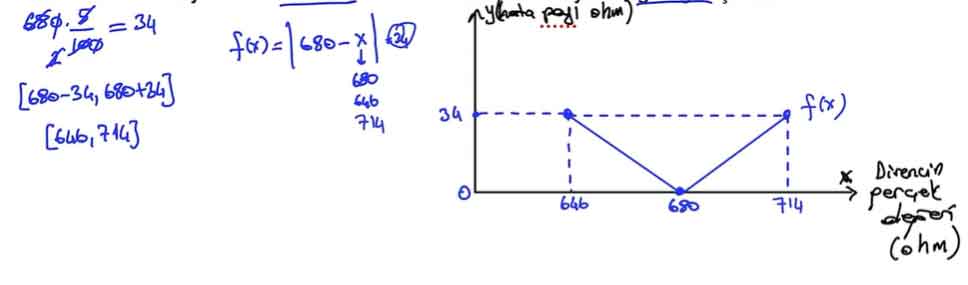
a- Elektrik devresi elemanları satışı yapan bir firma, 680 ohm ± %5 değerinde dirençler üretmektedir. Üretilen dirençlerin gerçek değerine (ohm) bağlı hata miktarının (ohm) değişimini ifade eden fonksiyonun cebirsel temsili nedir ve fonksiyonun grafiğini çiziniz?
Cevap:
- %5 hata miktarı: 680 x 0.05 = 34 ohm.
- Gerçek direnç değerleri aralığı: [680 - 34, 680 + 34] = [646, 714].
- Hata miktarını ifade eden fonksiyon:
f(x) = 680 - x - Grafik: Hata miktarının direnç değerine bağlı olarak azalan bir fonksiyon olduğu için negatif eğimli bir doğru elde edilir. Grafikte f(x) aralığı [646, 714] ile sınırlıdır.
b) Aşağıdaki tabloyu elde ettiğiniz f fonksiyonunun nitel özelliklerine göre uygun ifadelerle doldurunuz.
| Fonksiyonun Nitel Özellikleri | Değerler |
|---|---|
| Tanım Kümesi | [646, 714] |
| Görüntü Kümesi | [0, 34] |
| Fonksiyonun Sıfırı | x = 680 |
| Fonksiyonun İşareti | x < 680 için pozitif, x > 680 için negatif |
| Maksimum Nokta | (646, 34) |
| Minimum Nokta | (714, 0) |
| Bire Birliği | Fonksiyon bire bir değildir. |
| Artan veya Azalan Olduğu Aralıklar | x ∈ [646, 680] için azalan, x ∈ [680, 714] için artan |
2. Soru: Gerçek sayılarda f(x) = 1 - 2x ve g(x) = |f(x)| - 3 şeklinde tanımlı fonksiyonlar veriliyor. g fonksiyonuna göre aşağıdaki soruları cevaplayınız:
a) Görüntü kümesini bulunuz.
b) Sıfırlarını bulunuz.
c) Artan veya azalan olduğu aralıkları bulunuz.
ç) Minimum ve maksimum noktalarını bulunuz.
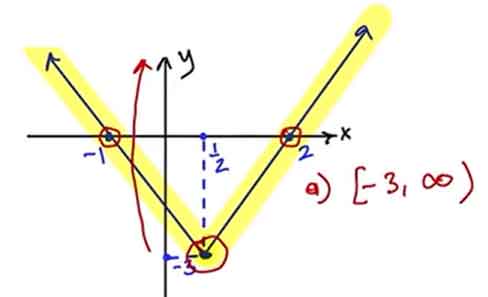
a) Görüntü Kümesini Bulunuz
Fonksiyonun mutlak değer ve sabit bir çıkarmaya dayandığı göz önünde bulundurulduğunda: g(x) = |f(x)| - 3 Mutlak değerden dolayı g(x)’in minimum değeri -3’tür ve üst sınırı yoktur.
Görüntü Kümesi: [-3, ∞)
b) Sıfırlarını Bulunuz
g(x) = 0 için:
|1 - 2x| - 3 = 0 → |1 - 2x| = 3
Bu mutlak değer denklemini çözerek:
1 - 2x = 3 → x = -1
1 - 2x = -3 → x = 2
Sıfır Noktaları: x = -1 ve x = 2
c) Artan veya Azalan Olduğu Aralıklar
x < 1/2 için fonksiyon azalandır.
x > 1/2 için fonksiyon artandır.
Aralıklar:
- Azalan: (-∞, 1/2)
- Artan: (1/2, ∞)
ç) Minimum ve Maksimum Noktalarını Bulunuz
Fonksiyonun minimum değeri, x = 1/2 noktasında alınır:
g(1/2) = |1 - 2(1/2)| - 3 = 0 - 3 = -3
Minimum Nokta: (1/2, -3)
Fonksiyonun bir maksimum noktası yoktur çünkü sonsuza kadar artar.
Maksimum Nokta: Yok





Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.