9. Sınıf Matematik 1. Ders Kitabı Sayfa 82-83-84-85-86-87 Cevapları Meb Yayınları

9. Sınıf Matematik – Ölçme ve Değerlendirme (Sayfa 82-87) Cevapları
1. Tema Ölçme ve Değerlendirme Soruları ve Cevapları
Sayfa 82 Cevapları
1. Aşağıdaki tabloda bazı gök cisimlerinin kütleleri (kg) yaklaşık olarak verilmiştir.
| Gök Cismi | Yaklaşık Kütlesi (kg) |
|---|---|
| Güneş | 1,99 × 10³⁰ |
| Dünya | 5,97 × 10²⁴ |
| Mars | 6,42 × 10²³ |
| Satürn | 5,68 × 10²⁶ |
| Ay | 7,34 × 10²² |
a) Dünya'nın kütlesinin Mars'ın kütlesinden kaç kg fazla olduğunu yaklaşık olarak bulunuz.
- Dünya'nın kütlesi: 5,97 × 10²⁴ kg
- Mars'ın kütlesi: 6,42 × 10²³ kg
Fark:
5,97 × 10²⁴ - 6,42 × 10²³
= (5,97 - 0,642) × 10²⁴
= 5,328 × 10²⁴ kg
Sonuç: Dünya’nın kütlesi, Mars’ın kütlesinden yaklaşık 5,33 × 10²⁴ kg fazladır.
b) Dünya, Mars ve Ay'ın kütleleri toplamının kaç kg olduğunu yaklaşık olarak bulunuz.
- Dünya: 5,97 × 10²⁴ kg
- Mars: 6,42 × 10²³ kg
- Ay: 7,34 × 10²² kg
Toplam:
5,97 × 10²⁴ + 6,42 × 10²³ + 7,34 × 10²²
= (5,97 + 0,642 + 0,0734) × 10²⁴
≈ 6,685 × 10²⁴ kg
Sonuç: Toplam kütle yaklaşık 6,69 × 10²⁴ kg olarak bulunur.
c) Güneş'in kütlesinin Dünya'nın kütlesinin kaç katı olduğunu yaklaşık olarak bulunuz.
- Güneş: 1,99 × 10³⁰ kg
- Dünya: 5,97 × 10²⁴ kg
Oran:
1,99 × 10³⁰ ÷ 5,97 × 10²⁴
= (1,99 ÷ 5,97) × 10³⁰⁻²⁴
≈ 3,33 × 10⁵
Sonuç: Güneş’in kütlesi, Dünya’nın kütlesinin yaklaşık 3,33 × 10⁵ katıdır.
d) Gerçek oranlara sadık kalınarak yapılan bir Güneş sistemi maketinde Satürn modelinin kütlesi 5,68 kg’dır. Bu makette Güneş modelinin kütlesi kaç kg olacaktır?
- Gerçek Satürn'ün Kütlesi: 5,68 × 10²⁶ kg
- Gerçek Güneş'in Kütlesi: 1,99 × 10³⁰ kg
Oran: 1,99 × 10³⁰ ÷ 5,68 × 10²⁶ ≈ 3,5 × 10³
Makette:
Satürn modelinin kütlesi 5,68 kg olduğuna göre:
Güneş modeli: 5,68 × 3,5 × 10³ ≈ 19,88 kg
Sonuç: Güneş modelinin kütlesi 19,88 kg olacaktır.
2. Semih Bey’in Bahçesi ve Otopark Hesaplamaları
Verilenler:
- Bahçenin alanı: 108 m²
- Otoparkın uzun kenarının uzunluğu, kısa kenarın uzunluğunun 2 katıdır.
- Bahçenin bir kenarının uzunluğu, otoparkın kısa kenar uzunluğunun 3 katıdır.
a) Bahçenin çevre uzunluğunu kaç metre olduğunu bulunuz.
Verilen: Bahçenin alanı 108 m².
Bahçe kare olduğuna göre:
Bir kenar uzunluğu: √108 = √(36 × 3) = 6√3 metre.
Çevre: Çevre = 4 × kenar uzunluğu = 4 × 6√3 = 24√3 metre.
Sonuç: Bahçenin çevre uzunluğu 24√3 metredir.
b) Otopark zemininin metrekaresi 550 TL olan taşlardan döşenecektir. Semih Bey’in toplam maliyetini hesaplayınız.
Verilen:
- Otoparkın kısa kenarı karenin bir kenarının 1/3’ü.
- Bahçenin kenarı: 6√3 metre.
- Otoparkın kısa kenarı: 6√3 ÷ 3 = 2√3 metre.
- Uzun kenar: 2 × kısa kenar = 2 × 2√3 = 4√3 metre.
Otopark Alanı: 2√3 × 4√3 = 24 m².
Maliyet:
Metrekare maliyeti 550 TL olduğuna göre:
24 × 550 = 13.200 TL.
Sonuç: Semih Bey’in otopark zemini için ödeyeceği toplam maliyet 13.200 TL olacaktır.
c) Semih Bey bahçesinin otopark dışında kalan bölümünü çitle çevirecektir. Bu alanın çevresi kaç metre olacaktır?
Çevre uzunluğu = 24√3 ≈ 41,57 m
Bu değer 41 ile 42 metre arasındadır.
Sonuç: 41 ve 42 arasında
Sayfa 83 Cevapları
3) A ve B şehirleri için Mart ayı sıcaklık bilgileri
- A şehrinde aylık ortalama sıcaklık 12 °C; herhangi bir anda ölçülen sıcaklık ortalamadan en fazla 8 °C sapabilir.
- B şehrinde aylık ortalama 7 °C; en düşük −2 °C, en yüksek 16 °C ölçülmüştür.
a) A ve B’de Mart ayı ölçülebilecek sıcaklık değerlerini mutlak değerli eşitsizlik ve aralık biçiminde yazınız.
-
A: |x − 12| ≤ 8 → [4, 20]
-
B: |x − 7| ≤ 9 → [−2, 16]
b) Hem A hem B’ye ait olabilecek sıcaklık değerleri (kesişim).
- Aralık: [4, 16]
- Küme gösterimi: A ∩ B = { x | 4 ≤ x ≤ 16, x ∈ ℝ }
- Sayı doğrusu: 4 ile 16 arası dolu (uçlar dolu noktalar).
c) A’ya ait olup B’ye ait olmayan sıcaklık değerleri (A \ B).
- Aralık: (16, 20]
- Küme gösterimi: A \ B = { x | 16 < x ≤ 20, x ∈ ℝ }
- Sayı doğrusu: 16’dan büyük 20’ye kadar, 20 dolu, 16 boş nokta.
ç) A’ya veya B’ye ait olabilecek sıcaklık değerleri (birleşim).
- Aralık: [−2, 20]
- Küme gösterimi: A ∪ B = { x | −2 ≤ x ≤ 20, x ∈ ℝ }
- Sayı doğrusu: −2 ile 20 arası komple dolu (uçlar dolu).
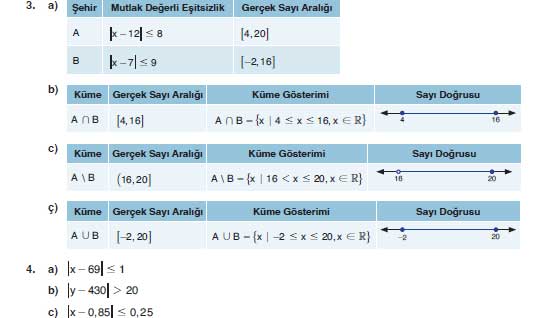
4) Futbol topu standartları (resmî müsabaka)
Tabloya göre izin verilen aralıkları mutlak değerli eşitsizlikle yazınız.
a) Çevre uzunluğu (cm)
- Standart aralık: 68 cm ≤ x ≤ 70 cm
- Mutlak değerli eşitsizlik: |x − 69| ≤ 1
b) Kütle (gram)
- Standart aralık: 410 g ≤ y ≤ 450 g
- “Olamayacağı” değerler (yani standart dışı): |y − 430| > 20
c) İç basınç (atm, deniz seviyesinde)
- Standart aralık: 0,60 atm ≤ p ≤ 1,10 atm
- Mutlak değerli eşitsizlik: |p − 0,85| ≤ 0,25
9. Sınıf Matematik – Ölçme ve Değerlendirme (Sayfa 84)
5. Soru – Reçel Fiyatı Belirleme
Soru: Evinde organik reçel yapan Zeynep Hanım, 1 kilogram reçelin fiyatını belirlemek istiyor. Piyasada satılan reçellerin fiyatlarını araştırdığında aşağıdaki tabloyu elde ediyor:
| Reçel Fiyatları (TL) | 184 | 145 | 220 | 175 | 130 | 155 | 134 | 225 |
Zeynep Hanım, belirleyeceği fiyatın ortalamadan en fazla 20 TL sapmasını istemektedir.
a) Zeynep Hanım’ın satış yapacağı 1 kg reçel fiyatının alacağı değerleri mutlak değerli eşitsizlik ile gösteriniz.
Cevap: |x − 171| ≤ 20
b) Zeynep Hanım’ın satış yapacağı 1 kg reçel fiyatının alabileceği en küçük ve en büyük değeri bulunuz.
Cevap: En küçük değer = 151 TL
En büyük değer = 191 TL
c) Zeynep Hanım’ın satış yapacağı 1 kg reçel fiyatının alabileceği değerleri sayı doğrusu üzerinde gösteriniz.
Cevap: 151 ve 191 uçları dâhil olacak şekilde [151, 191] aralığıdır.
ç) Tablodaki fiyatlardan hangileri bu aralığa dâhildir?
Cevap: 184 TL, 175 TL ve 155 TL bu aralıkta yer alır.
6. Soru – 100 Metre Koşusu Sıralama
Soru: Aşağıdaki tabloda 5 sporcunun 100 metre koşusundaki bitirme süreleri verilmiştir.
| Sporcu | Yarışı Bitirme Süresi (s) |
|---|---|
| Ali | 12,6a |
| Bora | 12,6b |
| Cem | 12,7c |
| Deniz | 12,7d |
| Efe | 12,7e |
Her sporcunun süresi birbirinden farklıdır. Süre ne kadar küçükse, derece o kadar iyidir.
a) Ali 1. olduysa a ve b rakamlarını sıralayınız.
Cevap: Ali’nin süresi Bora’dan küçük olmalıdır.
a < b
b) Bora 1. olduysa a’nın hangi değeri alamayacağını bulunuz.
Cevap: Bora 12,60 saniye ile 1. olur. Ali’nin süresi 12,6a olduğuna göre a, 0 olamaz.
a ≠ 0
c) Cem 3. ve Efe 5. olduysa c, d ve e rakamlarını sıralayınız.
Cevap: Cem’in süresi en küçük, Efe’ninki en büyük olduğundan:
c < d < e
9. Sınıf Matematik – Sayfa 85 (Soru 7 ve 8)
7. Soru – Kare Şeklindeki Oyun Kartı
Soru: Aşağıda kare şeklinde bir oyun kartı verilmiştir. Kartın yüzeyi kare ve dikdörtgen şeklindeki parçalara ayrılmıştır. Her bir parçanın bir kenar uzunluğu şekilde gösterilmiştir.
Buna göre aşağıdaki soruları cevaplayınız.
a) Oyun kartında verilen uzunluklardan yararlanarak (√3 + √2)² ifadesinin eşitini geometrik temsiller yardımıyla bulunuz.
Cevap: Kare, kenarı (√3 + √2) olan büyük bir karenin alanını temsil eder.
Her küçük şeklin alanını bulalım:
E = √3 × √3 = 3
F = √3 × √2 = √6
H = √2 × √3 = √6
J = √2 × √2 = 2
Toplam alan = 3 + √6 + √6 + 2 = 5 + 2√6
b) (√3 + √2)² ifadesinin eşitini gerçek sayılarda işlem özelliklerini kullanarak bulunuz.
Cevap: (√3 + √2)² = (√3)² + 2·√3·√2 + (√2)²
= 3 + 2√6 + 2
= 5 + 2√6
Her iki yöntemle de sonuç 5 + 2√6 bulunur.
8. Soru – ABCD Dikdörtgeni ve Park Alanı
Soru: Aşağıda verilen ABCD dikdörtgeni biçimindeki bir arsa, KLMN ve BCEL kareleri şeklinde iki parsele ayrılacaktır. Kalan kısmı yeşil alan, KLMN karesi ise çocuk parkı olarak düzenlenecektir.
|AK| = 2ˣ birim, |KL| = 2ˣ⁺¹ birim ve |LB| = 2ˣ⁺¹ − 1 birimdir.
Buna göre aşağıdaki soruları cevaplayınız.
a) Çocuk parkı olarak belirlenen bölgenin alanını x cinsinden ifade ediniz.
Cevap: KLMN bir kare olduğuna göre, kenar uzunluğu 2ˣ birimdir.
Alan = (2ˣ)² = 2²ˣ
b) Yeşil alan olarak belirlenen bölgenin alanını x cinsinden ifade ediniz.
Cevap: Toplam dikdörtgenin alanı:
Yükseklik = 2ˣ
Taban = (2ˣ + 2ˣ⁺¹ + 2ˣ⁺¹ − 1) = 5·2ˣ − 1
Toplam alan = (5·2ˣ − 1) × 2ˣ = 5·2²ˣ − 2ˣ
Yeşil alan = Toplam alan − Park alanı
= (5·2²ˣ − 2ˣ) − 2²ˣ
= 3·2²ˣ − 1
9. Sınıf Matematik – Sayfa 86 Cevapları
9. Soru: Alışveriş merkezinin otoparkında, sayı doğrusu üzerinde -5¹² ile 5¹² noktaları arasına eşit aralıklarla 20 adet park levhası yerleştirilmiştir.
Buna göre ardışık iki levha arası mesafe kaç birimdir?
Çözüm:
Toplam mesafe = 5¹² − (−5¹²) = 10·5¹²
Bu uzunluk 20 eşit aralığa bölünecek:
10·5¹² ÷ 20 = ½·5¹² = 5¹²⁄₂ = 6·5¹²
Cevap: 6·5¹²
10. Soru: Bir radyo istasyonu yayını en fazla 1,213×10⁵ metreye ulaşmaktadır.
Ayla: 6,84×10⁴ m
Burak: 1,3×10⁵ m
Ceren: 0,11×10⁶ m
Buna göre yayının kimlere ulaşacağını bulunuz.
Çözüm:
Ayla: 6,84×10⁴ = 0,684×10⁵ < 1,213×10⁵ → ulaşır
Burak: 1,3×10⁵ > 1,213×10⁵ → ulaşmaz
Ceren: 0,11×10⁶ = 1,1×10⁵ < 1,213×10⁵ → ulaşır
Cevap: Ayla ve Ceren
11. Soru: Verilen ispatta “x, y, z, t ∈ R ve x < y, z < t ise x − t < y − z olur.” önermesi adım adım gösterilmiştir.
Buna göre ilk hatanın yapıldığı adımı bulunuz.
Çözüm:
1. adım doğru.
2. adım doğru.
3. adımda çıkarılan sonuç, eşitsizliklerin yanlış toplanmasıyla elde edilmiştir.
Bu nedenle ilk hata 3. adımda yapılmıştır.
Cevap: 3. adım
9. Sınıf Matematik – Sayfa 87 Cevapları
12. Soru: Bir mağazada satılan pembe ve mavi tabureler üst üste dizilmiştir.
- Üst üste dizilen pembe ve mavi taburelerin yükseklikleri eşittir.
- Pembe taburelerin her birinin arasındaki mesafe Görsel 1’de,
- Mavi taburelerin her birinin arasındaki mesafe Görsel 2’de verilmiştir.
Depoda en fazla 20 pembe tabure üst üste dizilebilmektedir.
Buna göre en çok kaç mavi tabure üst üste dizilebilir?
Çözüm:
Pembe taburelerde yükseklik farkı: √256 = 16
Mavi taburelerde yükseklik farkı: √54 ≈ 7,35
Ayrıca mavi taburelerin aralığı pembe taburelere göre ¾ oranındadır.
Orantı kurarsak:
(20 – 1) × ¾ = 19 × ¾ = 14,25
Yaklaşık olarak 14 mavi tabure üst üste dizilebilir.
Cevap: C) 13
13. Soru: Aysun, Burak ve Canan tramvayla işe gitmektedir.
Biniş saatleri:
- Aysun: 07.25, süresi 35 dk
- Burak: 07.30, süresi 30 dk
- Canan: 07.40, süresi 40 dk
Üçü birlikte 8 dakika tramvayda bulunmuştur.
Buna göre aşağıdaki ifadelerden hangileri kesindir?
İfadeler:
I. En az ikisi birlikte 55 dk tramvayda bulundu.
II. İkisi birlikte 27 dk tramvayda bulundu.
III. Sadece biri 17 dk boyunca tramvayda bulundu.
Çözüm: Toplam süreler incelendiğinde, Aysun 07.25–08.00, Burak 07.30–08.00, Canan 07.40–08.20 arasında tramvaydadır.
Bu verilere göre I ve III doğru, II yanlıştır.
Cevap: D) I ve III







Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.