9. Sınıf Meb Matematik 1. Ders Kitabı 1. Tema Ek Ölçme ve Değerlendirme Soruları ve Cevapları

9. Sınıf Matematik – 1. Tema Ek Ölçme ve Değerlendirme (Sayfa 87)
Soru 1 – Robotlar
Verilen Bilgiler: A ve B noktaları arasında 13,5 birimlik bir yol vardır.
- 1. Robot, her saatte bir önceki saatte aldığı yolun 2 katı kadar yol alır.
- 2. Robot, her saatte bir önceki saatte aldığı yolun yarısı kadar yol alır.
- Robotlar karşı uca varınca beklemeden geri döner ve bu hareket döngüsel olarak devam eder.
a) Başlangıçtan itibaren her saatte alınan yolların tablosu
| Robot | 1. Saat | 2. Saat | 3. Saat | 4. Saat | n. Saat |
|---|---|---|---|---|---|
| 1. Robot | x | 2x | 4x | 8x | 2ⁿ⁻¹·x |
| 2. Robot | x | x/2 | x/4 | x/8 | x/2ⁿ⁻¹ |
b) “İki robot ilk kez 4. saatin başında birbirinden uzaklaşmaya başladı.”
Buna göre robotlar harekete başladıktan 2 saat sonra aralarındaki mesafe kaç birimdir?
Çözüm:
2 saatte her iki robotun birlikte yaklaştığı mesafe:
(1. robotun aldığı yol) + (2. robotun aldığı yol)
= (x + 2x) + (x + x/2)
= 3x + 1,5x
= 4,5x
Toplam mesafe 13,5 birim olduğuna göre:
13,5 − 4,5x = 3,6 birim
Cevap: 3,6 birim
c) Hızlı robotun (1. robot) harekete başladıktan 6 saat sonra başladığı noktaya uzaklığı kaç birimdir?
Çözüm:
1. robotun 6 saatte aldığı toplam yol:
x(1 + 2 + 4 + 8 + 16 + 32) = 63x
Yolun uzunluğu 13,5 birim olduğuna göre tam gidiş-dönüş uzunluğu:
2 × 13,5 = 27 birim
63x sayısı 27’ye bölündüğünde kalan:
63x mod 27 = 3,6 birim
Cevap: 3,6 birim
ç) x⁴ = y² olduğuna göre y’nin alabileceği değerlerin çarpımı nedir?
Çözüm:
x⁴ = y² ⇒ y = ±x²
Bu iki değerin çarpımı:
(+x²) × (−x²) = −x⁴
x⁴ = 216 / 225 olduğuna göre:
y₁ × y₂ = −x⁴ = −216 / 225
Cevap: −216 / 225
2. Soru Astronomide kullanılan uzaklık birimleri şunlardır:
Astronomik Birim (AB), Işık Yılı (IY), Parsek (pc) ve Kiloparsek (kpc).
Bu birimler, gök cisimlerinin birbirlerine olan uzaklıklarını ölçmede kullanılır.
Verilen Dönüşümler:
1 AB = 1,5×10⁸ km
1 IY = 1×10¹³ km
1 pc = 3,26×10¹³ km
1 kpc = 3,26×10¹⁶ km
Aşağıdaki tabloda Samanyolu galaksisinde bulunan bazı yıldızların Dünya’ya uzaklıkları verilmiştir:
| Yıldız Adı | Dünya’ya Uzaklığı (km) | Dünya’ya Uzaklığı (AB) | Dünya’ya Uzaklığı (IY) | Dünya’ya Uzaklığı (pc) |
|---|---|---|---|---|
| Spica | x | 2,62×10² | – | – |
| Betelgeuse | y | – | 1,3×10² | – |
| Castor | k | 3,44×10⁶ | – | – |
| Aldebaran | z | – | – | 2×10¹ |
a) x + k + z ifadesinin değerini bulunuz.
Yıldızların uzaklıklarını kilometreye çevirip topluyoruz.
Cevap: 3,788×10¹⁵ km
b) y / z ifadesinin değerini bulunuz.
Betelgeuse ve Aldebaran yıldızlarının uzaklıklarının oranı alınır.
Cevap: 6,5×10⁶
c) Tablodaki 4 yıldızı Dünya’ya olan uzaklıklarına göre yakından uzağa sıralayınız.
Cevap: Castor < Aldebaran < Spica < Betelgeuse
3. Soru Bir şehirde, ilk 25 m³ doğal gaz ücretsizdir.
Bir kullanıcının şubat ve mart ayına ait doğal gaz tüketimi aşağıda verilmiştir:
| Ay | İlk Okuma (m³) | Son Okuma (m³) | Ücret (TL) |
|---|---|---|---|
| Şubat | 92816 | 92941 | 674,5 |
| Mart | 92941 | 92998 | ? |
Soru: Kullanıcı mart ayında ne kadar doğal gaz ücreti ödemiştir?
Çözüm:
Şubat tüketimi: 92941 − 92816 = 125 m³
Ücretsiz miktar: 25 m³, ücretli miktar: 100 m³
→ Birim fiyat: 674,5 ÷ 100 = 6,745 TL/m³
Mart tüketimi: 92998 − 92941 = 57 m³
Ücretsiz miktar: 25 m³, ücretli miktar: 32 m³
→ Mart ücreti: 32 × 6,745 = 215,84 TL
Cevap: 215,84 TL
4. Soru – Havuzların Klorlanması
Soru: Aşağıda kenar uzunlukları eşit olan dikdörtgen biçiminde çocuk ve yetişkin havuzları verilmiştir.
Eşit kenar uzunlukları 25 m’dir.
Çocuk havuzunun uzun kenarı, yetişkin havuzunun uzun kenarının 3/5’i kadardır.
Yetişkin havuzunun uzun kenarı 30 m,
çocuk havuzunun derinliği d,
yetişkin havuzunun derinliği ise 3d’dir.
Çocuk havuzunu klorlamak için 1,0125×10⁷ mg klor kullanılmıştır.
Yetişkin havuzu için kullanılması gereken klor miktarı kaç mg’dır?
Çözüm:
- Çocuk havuzunun hacmi: 25 × (30×3/5) × d = 25 × 18 × d = 450d
- Yetişkin havuzunun hacmi: 25 × 30 × 3d = 2250d
- Hacim oranı: 2250d / 450d = 5
Klor miktarı hacimle orantılı olduğundan:
1,0125×10⁷ × 5 = 5,0625×10⁷ mg
Cevap: ➡️ Yetişkin havuzu için kullanılacak klor miktarı = 5,0625×10⁷ mg
5. Soru – Davet Mektupları
Soru: Bir eğitim kapsamında 7 farklı şehirden, her birinde seçilen 16 okul müdürüne davetiye gönderilecektir.
Ayrıca bu müdürlerin okullarındaki 27 öğretmene de birer davetiye gönderilecektir.
Bu davetiyeleri alan toplam kişi sayısının karesi A² ise, A kaçtır?
Çözüm:
- Müdür sayısı = 7 × 16 = 112
- Öğretmen sayısı = 112 × 27 = 3024
- Toplam kişi = 112 + 3024 = 3136
A² = 3136 olduğuna göre
A = 56
Cevap: ➡️ A = 56
6. Soru – Ayşe’nin Matematik Kampı Oyunu
Soru: Bir matematik kampında iki kutu vardır:
- 1. Kutu: 0,12 – 0,16 – 0,6
- 2. Kutu: 0,9 – 0,33 – 0,13
Ayşe birinci kutudan, diğer takım ikinci kutudan birer kart seçecektir.
Kurallar:
- Ayşe’nin seçtiği sayı, diğer takımdakinden büyükse, iki sayı çarpılır.
- Ayşe’nin seçtiği sayı, diğer takımdakinden küçükse, iki sayı toplanır.
- Her durumda karekökü alınır ve bulunan değer puan olur.
- Sonuç rasyonel sayı olmalıdır.
Çözüm:
En büyük puan: 0,16 + 0,33 = 0,49 = (0,7)² → √0,49 = 0,7
En küçük puan: 0,12² = 0,0144 → √0,0144 = 0,12
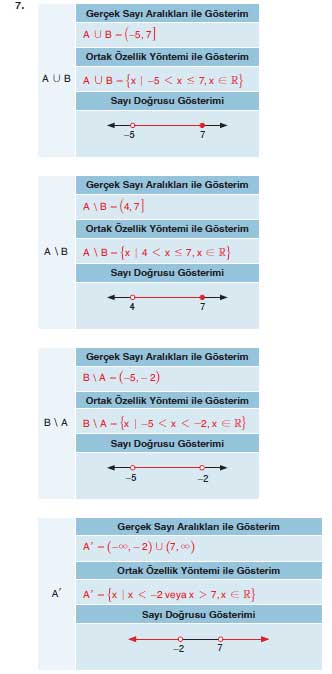
7. Soru: A = [-2, 7] ve B = (-5, 4] olsun.
Aşağıdaki tabloda verilen A ∩ B, A ∪ B, A \ B, B \ A ve A′ ifadelerinin farklı gösterim biçimlerini (gerçek sayı aralığı, ortak özellik yöntemi, sayı doğrusu) yazınız.
8. Soru – Ergenlik/Beyin gelişimi – yaş aralıkları
Soru: Aycan, Bora ve Ceyhun için verilen biyolojik gelişim bilgilerinden yararlanarak:
a) Her birinin şu anki yaşlarının girdiği gerçek sayı aralıklarını bulunuz.
b) Üç kişinin iki yıl sonraki yaşlarını kapsayan en dar aralığı mutlak değerli eşitsizlik olarak yazınız.
Cevap:
a)
- Aycan: (15, 19)
- Bora: (19, 21)
- Ceyhun: (21, 25)
b) İki yıl sonraki ortak aralık [17, 27] olur → merkez 22, yarıçap 5.
|x − 22| ≤ 5
9. Soru – Açlık kan şekeri aralıkları
Soru: Açlık kan şekeri için aralıklar: [49, 69] hipoglisemi, [70, 99] normal, [100, 130] gizli şeker.
Esra ve Engin’in ölçümleri sırasıyla x ve y olsun.
a) Esra’ya gizli şeker tanısı konduğuna göre x’i mutlak değerli eşitsizlikle yazınız.
b) Engin’e hipoglisemi tanısı konduğuna göre y’yi mutlak değerli eşitsizlikle yazınız.
Cevap:
a) Gizli şeker [100,130] → merkez 115, yarıçap 15: |x − 115| ≤ 15
b) Hipoglisemi [49,69] → merkez 59, yarıçap 10: |y − 59| ≤ 10
10. Soru – Sayı doğrusu ve aralık işlemleri
Soru: Aras’ın oyununda tavşan ve kedi sayı doğrusunda hareket etmektedir.
- Tavşan −1 noktasındadır, sağa doğru 8 birim gider → K = 7 noktasına ulaşır.
- Kedi −5 noktasındadır, sağa doğru 15 birim gider → N = 10 noktasına ulaşır.
Buna göre:
A = (−K, L) = (−7, 4)
B = [M, N] = [−11, 10] olsun.
a) A ∪ B kümesini aralık gösterimiyle yazınız.
b) (A \ B) ∪ (B \ A) kümesini aralık gösterimiyle yazınız.
c) Aras programı tekrar ettiğinde |K, 3L| ve (N, 2M] aralıklarının kesişimini bulunuz.
Cevap:
a) A ∪ B = [−11, 4]
b) (A \ B) ∪ (B \ A) = [−11, −5] ∪ [−3, 4]
c) |K, 3L| = [−7, 12] ve (N, 2M] = (10, −22]
→ Kesişim: [−7, 2]
11. Soru – Kare ve dikdörtgen alan ilişkisi
Soru: Şekil 1 ve Şekil 2’de kare ve dikdörtgenlerden oluşan şekiller verilmiştir.
a) Şekil 1’deki her bir dörtgenin alanını bulunuz ve toplayınız.
b) Şekil 2’de kenar uzunluğu (a + b) olan karenin alanını bulunuz.
c) a ve b maddelerinde bulunan ifadeler arasındaki eşitliği yazınız.
Cevap:
a) Şekil 1’deki dört dikdörtgenin alanı:
a² + ab + ab + b² = a² + 2ab + b²
b) Şekil 2’deki karenin alanı:
(a + b)²
c) (a + b)² = a² + 2ab + b²
→ Bu iki ifade birbirine eşittir, yani cebirsel özdeşliktir.
12. Soru Aşağıda mavi ve kırmızı renkli pullardan oluşan bir örtüntünün ilk üç adımı verilmiştir.
Buna göre bu örtüntünün:
a) 10. adımındaki mavi renkli pulların sayısını bulunuz.
b) n. adımındaki mavi renkli pulların sayısına ait cebirsel ifadeyi elde ediniz.
Cevap:
Her adımda mavi pullar 8’er tane artmaktadır.
İlk adımda 24 mavi pul vardır.
a) 10. adım = 24 + (10 – 1) × 8 = 96
b) n. adım formülü: 8n + 16
13. Soru Kalınlığı 0,7 mm olan bir kâğıt 12 defa katlanabilseydi kalınlığının x metre,
kalınlığı 0,2 mm olan bir kâğıt 9 defa katlanabilseydi kalınlığının y metre olacağı hesaplanıyor.
Buna göre x değeri, y değerinin kaç katıdır?
A) 28 B) 30 C) 32 D) 34 E) 36
Çözüm: Katlama her defasında kalınlığı 2 katına çıkarır.
x / y = (0,7 × 2¹²) / (0,2 × 2⁹) = (0,7 / 0,2) × 2³ = 3,5 × 8 = 28
Cevap: A) 28
14. Soru Everest Dağı’nın yüksekliğinin yaklaşık 8850 m olduğu bilinmektedir.
Everest Dağı’nın yüksekliğine ulaşmak için kalınlığı 0,5 mm olan kâğıtlardan kaç adet kullanılması gerektiği hesaplanmak isteniyor.
Bu işlemi yapan kişi, gereken kâğıt sayısının bilimsel gösterimini aşağıdakilerden hangisi olarak yazmalıdır?
A) 2,45 × 10⁶ B) 2,45 × 10⁷ C) 1,77 × 10⁷ D) 17,7 × 10⁷ E) 2,45 × 10⁸
Çözüm:
Kâğıt kalınlığı = 0,5 mm = 0,0005 m
Everest yüksekliği = 8850 m
Kâğıt sayısı = 8850 / 0,0005 = 17.700.000 = 1,77 × 10⁷
Cevap: C) 1,77 × 10⁷
15. Soru Uzun kenar uzunluğunun kısa kenar uzunluğuna oranı √3 olan eş dikdörtgenler, Şekil 1 ve Şekil 2’deki gibi yerleştiriliyor.
Şekil 1’de toplam uzunluk 14 cm, Şekil 2’de ise 16 cm’dir.
Soru: Buna göre bu dikdörtgenlerden birinin çevresi kaç cm’dir?
Çözüm: Kısa kenara x, uzun kenara √3x diyelim.
Şekil 1 için: 14 = √3x + 2x
Şekil 2 için: 16 = 2√3x + x
Bu iki denklemi birlikte çözdüğümüzde x = 5(√3 - 1) bulunur.
Bir dikdörtgenin çevresi:
Çevre = 2(x + √3x) = 2x(1 + √3)
= 2 × 5(√3 - 1)(1 + √3)
= 10(3 - 1)
= 20
Cevap: 20
16. Soru Tahtada soldan sağa doğru büyükten küçüğe sıralı dört sayı vardır:
-
sayı 2⁷, 2. sayı A, 3. sayı 2⁶, 4. sayı B.
Verilen bilgiler:
1️⃣ 1. sayı ile 2. sayı arasındaki fark, 2. ile 3. sayı arasındaki farkın 3 katıdır.
2️⃣ 3. sayı ile 4. sayı arasındaki fark, 1. ile 2. sayı arasındaki farkın yarısıdır.
Buna göre A + B kaçtır?
Çözüm: 2⁷ = 128, 2⁶ = 64
128 - A = 3(A - 64)
128 - A = 3A - 192
320 = 4A → A = 80
64 - B = ½(128 - 80) = 24 → B = 40
A + B = 80 + 40 = 120
Cevap: 120




Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.