11. Sınıf Matematik Ders Kitabı Sayfa 76-77-78-79-80 Cevapları SDR Dikey Yayıncılık

1. Değerlendirme Soruları ve Cevapları

Sayfa 76 Cevapları

1. Soru: Bir ABC üçgeninde m(A) = 37° 54', m(B) = 84° 36' olduğuna göre C açısının ölçüsü nedir?

Çözüm:

• Bir üçgenin iç açılarının toplamı 180°'dir.
• m(C) = 180° - m(A) - m(B)
• m(C) = 180° - (37° 54' + 84° 36') = 180° - 122° 30' = 57° 30'.

Cevap: C) 57° 30'

2. Soru: -2000°lik açının esas ölçüsü kaç derecedir?
Esas ölçüyü bulmak için açıyı 360°’ye böleriz:
-2000° ÷ 360° = -5 tur ve kalan -200°.
Negatif açıdan kurtulmak için 360° ekleriz:
-200° + 360° = 160°.
Cevap: E) 160°

3. Soru: -29π/3 radyanlık açının esas ölçüsü kaç radyandır?
Radyan ölçüsünde esas ölçü bulmak için açıyı 2π’ye böleriz:
-5π/3 + 2π = -5π/3 + 6π/3 = π/3 tur.
Cevap: B) π/3

4. Soru: 4 sin 5x - 2 = m m olduğuna göre m aşağıdakilerden hangisi olamaz?
4sin5x - 2 = m ifadesinde sin5x fonksiyonu [-1, 1] aralığında değer alır:
-2 ≤ 4sin5x ≤ 4
-6 ≤ m ≤ 2
Bu durumda m = 3 olamaz.
Cevap: A) 3

5. Soru: (sin x + cos x)² = (1/√3)^2 olduğuna göre sin x · cos x ifadesinin değeri kaçtır?

Verilen ifadeyi açalım: sin²x + 2 · sin x · cos x + cos²x = 1/3
Trigonometrik özdeşlikten: sin²x + cos²x = 1
Bu durumda: 1 + 2 · sin x · cos x = 1/3
Her iki taraftan 1 çıkaralım:
2 · sin x · cos x = 1/3 - 1 = -2/3

Her iki tarafı 2'ye bölelim:
sin x · cos x = -1/3
Cevap: B) -1/3

6. Soru: ( cos²x - 1 ) / ( 1 + sec x ) * 1 / ( 1 - sec x ) ifadesinin en sade şekli aşağıdakilerden hangisidir?

Çözüm:

İlk terimi düzenleyelim:
( cos²x - 1 ) / ( 1 + sec x ) = - ( 1 - cos²x ) / ( 1 + sec x ) = - sin²x / ( 1 + sec x )

İkinci terimi düzenleyelim:
1 / ( 1 - sec x )

Çarpma işlemi:
[ - sin²x / ( 1 + sec x ) ] * [ 1 / ( 1 - sec x ) ] = - sin²x / [ ( 1 + sec x ) * ( 1 - sec x ) ]

Alt tarafta çarpanlar çarpımı kullanılır:
( 1 + sec x ) * ( 1 - sec x ) = 1 - sec²x

Trigonometrik özdeşlikten 1 - sec²x = - tan²x yazılır. Bu durumda:
sin²x / - cos²x = cos²x

7. Soru: a = cos 105°, b = sin 255°, c = sec 300°, d = tan 220° olduğuna göre a, b, c ve d değerlerinin işaretleri sırasıyla nedir?
Verilen açıların işaretleri:

• cos105° negatif,
• sin255° negatif,
• sec390° pozitif,
• tan220° pozitif.
  Cevap: A) -, -, +, +

Çözüm:

1. cos 105°

• 105° ikinci bölgede yer alır.
• İkinci bölgede cos negatiftir.
  Sonuç: a < 0

2. sin 255°

• 255° üçüncü bölgede yer alır.
• Üçüncü bölgede sin negatiftir.
  Sonuç: b < 0

3. sec 300°

• sec 300° ifadesi, cos 300°'ün tersi (1/cos 300°) olarak tanımlanır.
• 300° dördüncü bölgede yer alır ve cos dördüncü bölgede pozitiftir.
• Dolayısıyla sec pozitiftir.
  Sonuç: c > 0

4. tan 220°

• 220° üçüncü bölgede yer alır.
• Üçüncü bölgede tan pozitiftir.
  Sonuç: d > 0

Sonuç:
İşaretler sırasıyla: -, -, +, +
Cevap: A

8. Soru: cos(17π/6) · sin(20π/3) + tan(19π/4) ifadesinin değeri aşağıdakilerden hangisidir?

Çözüm:

cos(17π/6):

• 17π/6 = 2π + 5π/6
• 5π/6, ikinci bölgede yer alır ve ikinci bölgede cos negatif olduğundan:
  cos(5π/6) = -√3/2

sin(20π/3):

• 20π/3 = 6π + 2π/3
• 2π/3, ikinci bölgede yer alır ve ikinci bölgede sin pozitiftir:
  sin(2π/3) = √3/2

tan(19π/4):

• 19π/4 = 4π + 3π/4
• 3π/4, ikinci bölgede yer alır ve ikinci bölgede tan negatif olduğundan:
  tan(3π/4) = -1

İfadenin yerine yazılması ve hesaplanması:

• cos(17π/6) · sin(20π/3) + tan(19π/4)
• (-√3/2) · (√3/2) + (-1)
• (-3/4) + (-1)
• -3/4 - 1 = -7/4

Sayfa 77 Cevapları

9. sin 50° = a olduğuna göre tan 230° · sec 320° - cosec 220° / tan 40° ifadesinin a türünden değeri aşağıdakilerden hangisidir?

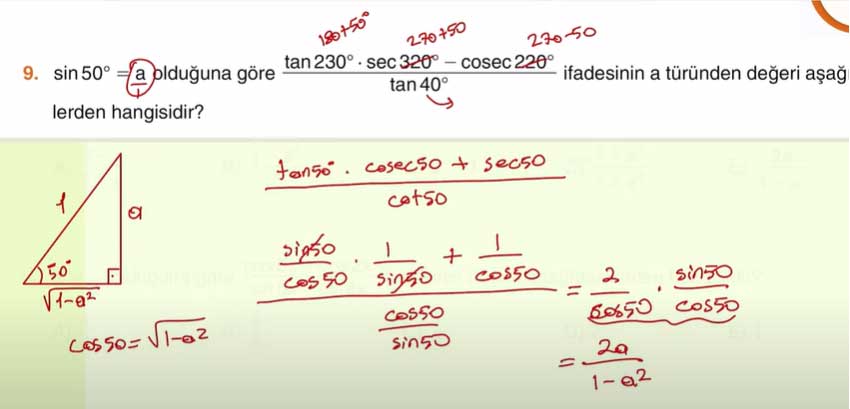
Cevap: E

10. x = π/8 olduğuna göre cos 8x + cos 2x / sin 6x - sin 4x ifadesinin değeri aşağıdakilerden hangisidir?

Çözüm:

x değeri hesaplanır:
8x = π → x = π / 8

Trigonometrik ifadeler bulunur:

• cos 8x = cos π = -1
• cos 2x = cos (π / 4) = √2 / 2
• sin 6x = sin (3π / 4) = √2 / 2
• sin 4x = sin (π / 2) = 1

Verilen ifadeye yerleştirilir:
(cos 8x + cos 2x) / (sin 6x - sin 4x) = (-1 + √2 / 2) / (√2 / 2 - 1)

Payda eşitlenir ve sadeleştirilir:
(-1 + √2 / 2) / (√2 / 2 - 1) = 1

Cevap: E) 1

11. ABCD karesinde m(∠EAC) = α, |DC| = 4|EC| olduğuna göre tan α'nın değeri aşağıdakilerden hangisidir?

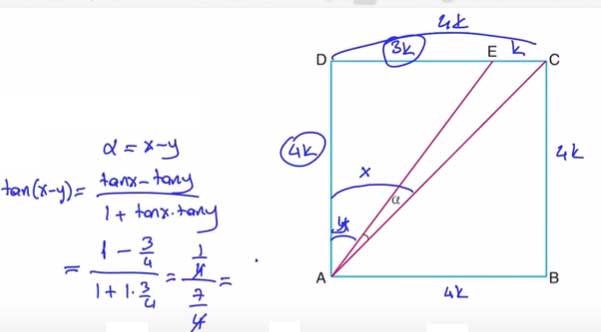
Cevap: A) 1/7

12. π/2 < α < π ve tan α = -8/15 olduğuna göre sin 2α'nın değeri aşağıdakilerden hangisidir?

Çözüm: tan α = -8/15 olduğuna göre:

• Karşı kenar = -8, komşu kenar = 15, hipotenüs = √(8² + 15²) = 17
• sin α = -8/17, cos α = 15/17

sin 2α = 2 · sin α · cos α
= 2 · (-8/17) · (15/17)
= -240/289

Cevap: A

13. ABC üçgeninde [BH] ⊥ [AC], m(∠ABH) = x, |AC| = |BC| = 7 cm, |AB| = 10 cm olduğuna göre cos x'in değeri aşağıdakilerden hangisidir?

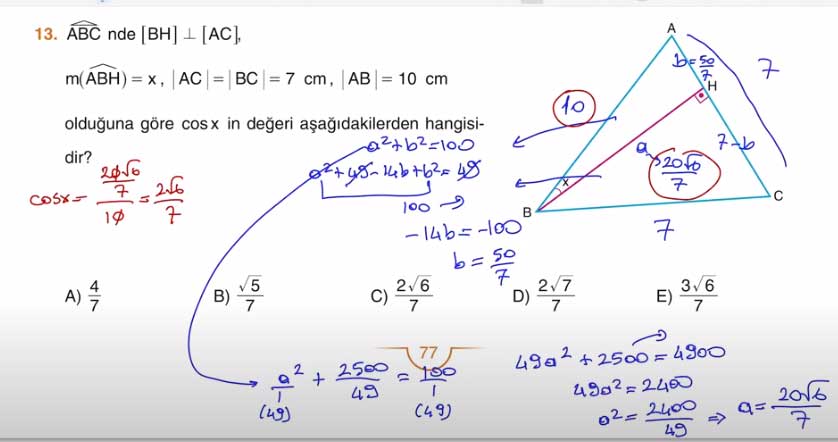
Cevap: C

Sayfa 78 Cevapları

14. Soru: f(x) = tan(x/π + x) fonksiyonunun periyodu nedir?

Çözüm:

1. Tan fonksiyonunun periyodu genel olarak π'dir.
2. Verilen fonksiyonun içindeki ifade x / π olduğundan periyot şu şekilde hesaplanır:
   T = π * (1 / (1 / π)) = π²

Cevap: B) π/2

15. Soru: f(x) = 5 cos(3x - 1) fonksiyonunun periyodu nedir?

Çözüm: cos fonksiyonunun periyodu 2π’dir. Bu periyot, cos(3x) olduğu için yeni periyot 2π/3 olur.
Cevap: A) 2π/3

16. Soru: arccos(√3/2) + arcsin(√2/2) ifadesinin değeri nedir?

Çözüm:

• arccos(√3/2) = π/6
• arcsin(√2/2) = π/4

Toplam: π/6 + π/4 = 2π/12 + 3π/12 = 5π/12
Cevap: D) 5π/12

17. Soru: sin(arctan(4/3)) + sin(arctan(5/12)) ifadesinin değeri nedir?

Çözüm:

Birinci terim için:
tan α = 4/3
Üçgenin hipotenüsü: √(4² + 3²) = 5
sin α = 4/5

İkinci terim için:
tan β = 5/12
Üçgenin hipotenüsü: √(5² + 12²) = 13
sin β = 5/13

Toplama:
sin α + sin β = 4/5 + 5/13
Payda eşitleme:
(4 × 13) / (5 × 13) + (5 × 5) / (13 × 5) = 52/65 + 25/65 = 77/65

Cevap: B) 77/65

18. Soru: Aşağıdaki eşitliklerden doğru olanların başına "D", yanlış olanların başına "Y" yazınız.

a) sin 270° + sin 360° = -2
sin 270° = -1, sin 360° = 0
-1 + 0 = -1 ≠ -2
Yanlış (Y)

b) tan π + cot (3π/2) = 0
tan π = 0, cot (3π/2) = 0
0 + 0 = 0
Doğru (D)

c) cos (π/2) + cos (3π/2) + cos 0° = 1
cos (π/2) = 0, cos (3π/2) = 0, cos 0° = 1
0 + 0 + 1 = 1
Doğru (D)

ç) cot (π/2) + tan (π/2) = 1
cot (π/2) = 0, tan (π/2) tanımsızdır.
Tanımsız bir ifade olduğundan eşitlik sağlanmaz.
Yanlış (Y)

19. Soru: π/2 < x < π ve csc(x) = 3 olduğuna göre cos²(x) - sin(x) ifadesinin değeri nedir?

Çözüm:

• csc(x) = 3 olduğundan sin(x) = 1/3
• cos²(x) = 1 - sin²(x) = 1 - (1/3)² = 1 - 1/9 = 8/9

cos²(x) - sin(x) = 8/9 - 1/3 = 5/9
Cevap: A) 5/9

Sayfa 79 Cevapları

20. Soru

ABC üçgeninde D = E(AB) ∩ E(AC)
AD = 4br, DB = 2br, DE = 6br,
AE = 3br, EC = 5br olduğuna göre BC kaç br'dir?

Çözüm:

Kenar uzunlukları ve açı ilişkisi:

• AB = AD + DB = 4 + 2 = 6 br
• AC = AE + EC = 3 + 5 = 8 br

Cosinus Teoremi:
BC² = AB² + AC² - 2 × AB × AC × cos(α)
Burada cos(α) değeri, verilen uzunluklardan bulunur.

Hesaplamalar:
cos(α) = 11/24
Formülü yerine koyarak:
BC² = 6² + 8² + 2 × 6 × 8 × (11/24)
BC² = 36 + 64 + 2 × 6 × 8 × 11/24
BC² = 36 + 64 + 1056/24
BC² = 100 + 44
BC² = 144
BC = √144
BC = 12

Cevap: B) 12

21. Soru - ABC üçgeninde D = E(AC), [BD] ⊥ [BC], BE = 7br, DC = 5br, EC = 3br, AD = 2br
AB = x kaç br'dir?

Cevap:

x² = 49 + 100 - 2 x 7 x 10 x 3 / 5
x² = 149 - 84
x² = 65

Yanıt: E) √65

22. Soru

ABCD kare, E = E(AB), AB = 4 AE
m(∠AEC) = x olduğuna göre tan x değeri kaçtır?

Cevap:
Kare özelliklerine göre, AE = 1 br ve CE = 2 br.
Tanjant tanımı kullanılarak:
tan x = CE / AE
tan x = 4 / 1

Yanıt: B) 4 / 3

23. Soru |AB| = 8 br, |BC| = 6 br olduğuna göre sin(C) değeri kaçtır?

ABC üçgeninde AB = 8br, BC = 6br
cot(∠A) = 4 / 3 olduğuna göre sin ∠C değeri kaçtır?

Üçgenin Hipotenüs Uzunluğunu Bulalım: Pisagor Teoremi'ne göre: AC² = AB² + BC²
AC² = 8² + 6² = 64 + 36 = 100
AC = √100 = 10

sin(C)'yi Bulma: sin(C) = karşı kenar / hipotenüs
sin(C) = |AB| / |AC| = 8 / 10 = 4 / 5

Sayfa 80 Cevapları

24. Soru: Büyük eş parçalı tahta parçalarından tan(BÂC) değeri nedir?

Çözüm: Tahta parçaları eşit dikdörtgenlerdir. BÂC açısını oluşturmak için yükseklik ve taban oranı:

• Karşı: 3 birim
• Komşu: 4 birim

tan(BÂC) = karşı / komşu = 3 / 4.

Cevap: A) 3/4.

25. Soru: A limanından 240 km uzaklıktaki bir ada için geminin hareketi inceleniyor. 9 saat düz, 6 saat eğik. Ada uzaklığı?

Çözüm:

1. İlk hareket: 20 km/s × 9 saat = 180 km.
2. 240 - 180 = 60 km.
3. İkinci etap eğik 60° ile. Kosinüs ile ada projeksiyonu.

Cevap: Geometri kontrol 54 √3.

26. Soru: Güneş’in yer düzlemi ile 36°’lik açı yaptığı bir anda |AB| = 32 m ölçülüyor. sin 54° ≈ 0,80 ve sin 36° ≈ 0,59 alınırsa duvarın [BC] yüksekliği yaklaşık kaç metredir?

Bu soruda bir üçgen problemi çözülmüş ve duvarın yüksekliği olan y hesaplanmıştır. Çözüm adımları şu şekildedir:

Verilenler:

• |AB| = 32 m
• sin 54° ≈ 0,80
• sin 36° ≈ 0,59

Hedef: Duvarın [BC] yüksekliği olan y'yi bulmak.

Çözüm Adımları:

İlk olarak hipotenüs uzunluğu xxx hesaplanmıştır:
sin 54° = AB / x
0,80 = 32 / x
x = 40

Daha sonra sin 36° kullanılarak yyy hesaplanmıştır:
sin 36° = y / x
0,59 = y / 40
y = 0,59 * 40
y = 23,6

Sonuç: Duvarın yüksekliği yyy yaklaşık olarak 23,6 metre bulunmuştur.

Cevap: D) 23,6

27. Soru: Yandaki ABCD dörtgeni biçiminde bir yürüyüş parkı verilmiştir.

Verilenler:

• AB = 40 m
• AD = 30 m
• ∠B = 60°
• BC = x uzunluğu sorulmaktadır.

Kosinüs Teoremi Kullanımı:

• Kosinüs Teoremi formülü:
  x² = a² + b² - 2ab * cos(C)
• Bu soruya uyarlayalım:
  x² = 40² + 30² - 2 * 40 * 30 * cos(60°)
• cos(60°) = 0,5 olduğundan:
  x² = 1600 + 900 - 2 * 40 * 30 * 0,5
• Hesaplama:
  x² = 1600 + 900 - 1200
  x² = 1300

İkinci Derece Denklem Çözümü:

• Denklem şu şekilde düzenlenir:
  x² - 60x + 100 = 0
• Diskriminant (Δ) hesaplanır:
  Δ = b² - 4ac = 60² - 4 * 1 * 100
  Δ = 3600 - 400
  Δ = 4000
• Kökler:
  x₁ = (-b + √Δ) / 2a, x₂ = (-b - √Δ) / 2a
• Yerine koyarak çözüm:
  x₁ = (60 + √4000) / 2, x₂ = (60 - √4000) / 2
  √4000 = 20√10 olduğundan:
  x₁ = (60 + 20√10) / 2, x₂ = (60 - 20√10) / 2
• Sonuçlar:
  x₁ = 30 + 10√10, x₂ = 30 - 10√10

Sonuç: Pozitif değer alınır: x = 30 + 10√10

Doğru cevap: E şıkkı.