Meb Yayınları 9. Sınıf Matematik 1. Ders Kitabı Sayfa 109 Sıra Sizde Cevapları

Sorular ve Cevaplar

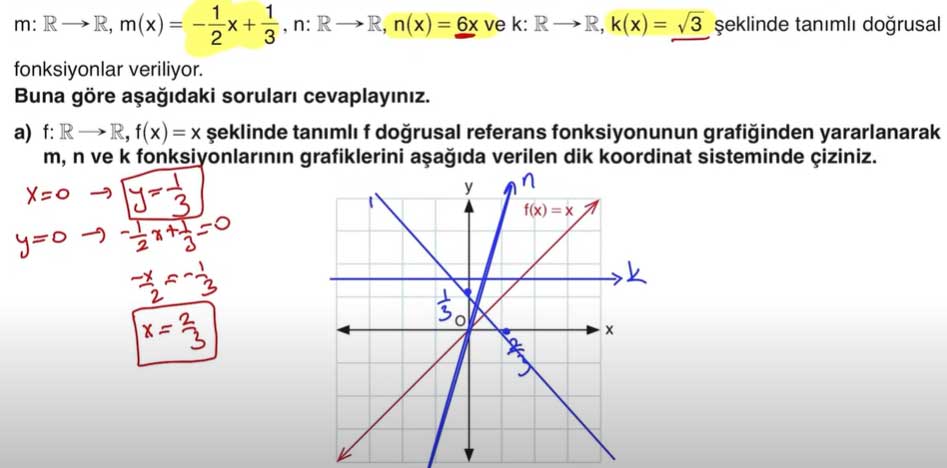
a) f: R → R, f(x) = x şeklinde tanımlı doğrusal referans fonksiyonunun grafiğinden yararlanarak m, n ve k fonksiyonlarının grafiklerini aşağıda verilen dik koordinat sistemine çiziniz.

Cevap: Grafikler şu şekilde çizilir:

f(x) = x: Eğim a = 1, y-eksenini 0'da keser.
m(x) = -1/2x + 1/3: Eğim a = -1/2, y-eksenini 1/3'te keser.
n(x) = 6x: Eğim a = 6, y-eksenini 0'da keser.
k(x) = √3: Sabit bir fonksiyondur ve grafiği y = √3 doğrusu olarak çizilir.

b) Çizdiğiniz grafiklerden yararlanarak m, n ve k fonksiyonlarına ait grafiklerin eğimini bulunuz. Bulduğunuz eğim değerlerini f fonksiyonuna ait grafik eğimi ile karşılaştırınız.

m(x): Eğimi -1/2 olup, bu negatif bir eğimdir. Grafiği x eksenine daha yakındır.
n(x): Eğimi 6 olup, pozitif bir eğimdir. Grafiği y eksenine daha dik bir şekilde yaklaşır.
k(x): Sabit bir fonksiyon olduğu için eğimi 0'dır. x eksenine pareleldir.

Karşılaştırma:

f(x) fonksiyonunun eğimi diğer fonksiyonlarla karşılaştırıldığında pozitif ve orta bir eğime sahiptir.
m(x) grafiği negatif eğimli olup x eksenine daha yakın ilerler.
n(x) grafiği ise pozitif ve oldukça dik bir eğime sahiptir.
k(x) grafiği sabit olduğundan eğimi yoktur.

Eğrilerin özelliklerini anlamak için grafiklerin x ve y eksenine olan uzaklıklarını göz önünde bulundurabilirsiniz.

c) m, n ve k fonksiyonlarının sıfırını, fonksiyonların temsil eden grafiklerin y-eksenini kestikleri noktaları, maksimum ve minimum değerlerini bulunuz.

m(x):

Sıfır: m(x) = 0 için x = 2/3.
Y-eksenini kestiği nokta: (0, 1/3).
Maksimum ve minimum değer: Yok.

n(x):

Sıfır: n(x) = 0 için x = 0.
Y-eksenini kestiği nokta: (0, 0).
Maksimum ve minimum değer: Yok.

k(x):

Sabit fonksiyon olduğu için sıfır yoktur.
Y-eksenini kestiği nokta: (0, √3).
Maksimum ve minimum değer: Sabit olduğundan √3.

ç) Fonksiyonların artan veya azalan olduğu aralıkları bulunuz.

f(x): Tüm gerçek sayılarda artandır.
m(x): Tüm gerçek sayılarda azalır.
n(x): Tüm gerçek sayılarda artandır.
k(x): Sabit fonksiyon olduğundan artma ya da azalma durumu yoktur.

d) Fonksiyonların bire bir olup olmadıklarını belirleyiniz.

f(x): Bire birdir.
m(x): Bire birdir.
n(x): Bire birdir.
k(x): Sabit fonksiyon olduğundan bire bir değildir.

e) Fonksiyonların artanlık-azalanlık ve bire birliği ile ilgili ulaştığınız sonuçları bire birlik ve artanlık-azalanlık tanımlarından yararlanarak cebirsel olarak doğrulayınız.

Artanlık-Azalanlık: