9. Sınıf Matematik 2. Ders Kitabı Sayfa 138-139 Cevapları Meb Yayınları

5. Sıra Sizde

a) Üç basamaklı bir doğal sayının 8’e tam bölünüp bölünmediğini gösteren bir önerme yazıp bu önermenin doğruluğunu ispatlayınız.

Önerme: Bir üç basamaklı sayı olan abc sayısı, 100a + 10b + c şeklinde yazılır. Bu sayı, 8 ile tam bölünebiliyorsa, şu eşitlik sağlanır:
100a + 10b + c = 8k (k ∈ N)

Bu ifadeyi parçalara ayıralım:
100a + 10b + c = 96a + 8b + (4a + 2b + c)
Burada 96a + 8b kısmı zaten 8’e tam bölünür.
Geriye kalan (4a + 2b + c) ifadesi de 8'e tam bölünüyorsa, o hâlde sayı 8’in katı olur.

Yani:
abc 8 ile tam bölünür ⇔ (4a + 2b + c) ≡ 0 (mod 8)
Böylece, sayının 8'e tam bölünebilmesi için bu koşul yeterlidir.

b) Önermeyi ispatlamak için kullandığınız mantık bağlaçları ve niceleyicilere yönelik çıkarımlarınız ne olur? Açıklayınız.

Kullanılan bağlaç:
İspatta “⇒” (ise) bağlacı kullanılmıştır.
Bu bağlaç, “Eğer (4a + 2b + c) 8’in katı ise, sayı 8’e tam bölünür” mantığını ifade eder.
Ayrıca ∀ (tüm üç basamaklı sayılar için) evrensel niceleyici dolaylı olarak kullanılmıştır.

Açıklama: İspatta kullanılan mantıksal yapılar algoritmanın doğruluğunu test etmede büyük önem taşır.
Örneğin, (4a + 2b + c) % 8 == 0 şartı sağlandığında sayı 8'e bölünür sonucuna ulaşılır.

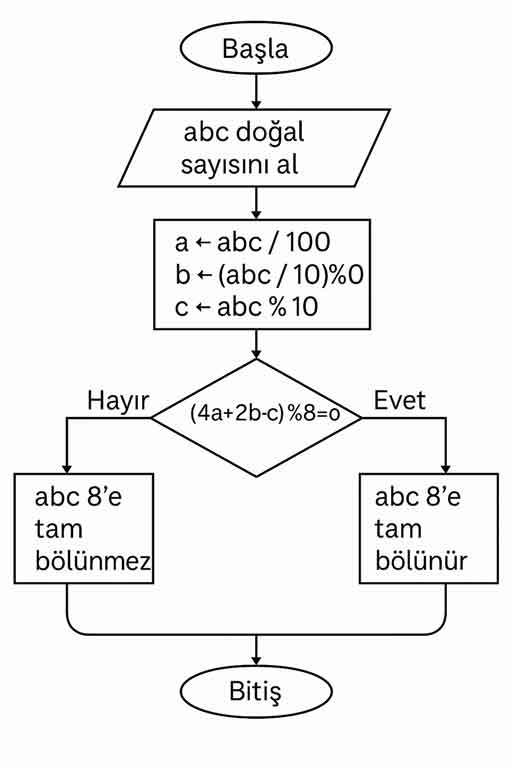
c) İspat adımlarından hareketle üç basamaklı bir doğal sayının 8’e tam bölünüp bölünmediğini bulan bir algoritmanın işleyişini akış şeması ile ifade ediniz.

11. Uygulama

Bir Cebirsel İspatın Algoritmik Yaklaşımla İncelenmesi
Aşağıdaki soruları cevaplayınız.

1. Cebirsel İspat:

Önerme:

∀a > 0 için f: ℝ → ℝ, f(x) = ax + b fonksiyonu artan bir fonksiyondur.

İspat:

1. Tanım: Bir fonksiyonun artan olması için
   x₁ < x₂ ⇒ f(x₁) < f(x₂) şartı sağlanmalıdır.

2. f(x) = ax + b olsun, burada a > 0.

3. x₁, x₂ ∈ ℝ ve x₁ < x₂ olduğunu varsayalım.

4. f(x₁) = a·x₁ + b
   f(x₂) = a·x₂ + b

5. f(x₁) < f(x₂) ⇔ a·x₁ + b < a·x₂ + b

6. Her iki taraftan da b çıkarılır:
   a·x₁ < a·x₂

7. a > 0 olduğundan dolayı:
   x₁ < x₂ ⇒ f(x₁) < f(x₂) olur.

Sonuç: Bu durumda, f(x) = ax + b fonksiyonu a > 0 için artan bir fonksiyondur.

2. Sözel Açıklama:

Fonksiyonun artan olduğunu göstermek için iki farklı girdi alırız. Bu girdilerin küçükten büyüğe sıralandığında çıktılarının da aynı sırada olması gerekir. a > 0 olduğundan çarpma işleminde yön değişmez. Bu nedenle fonksiyon artandır.

Cebirsel İspatın Sözel İfadesi:

Her x₁ ve x₂ reel sayısı için, eğer x₁ < x₂ ise, bu sayıların görüntüleri olan f(x₁) ve f(x₂) karşılaştırıldığında f(x₁) < f(x₂) oluyorsa, f(x) fonksiyonu artandır.

Bu tanıma göre, f(x) = ax + b fonksiyonu için, eğer a > 0 koşulu sağlanıyorsa, f(x) fonksiyonu artan olur. Çünkü bu durumda x arttıkça f(x) de artar.

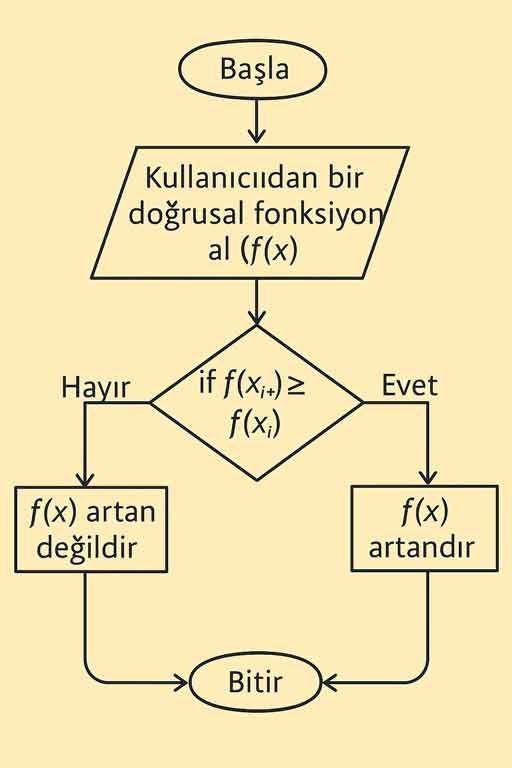
3. Elde ettiğiniz sözel ifadelerden faydalanarak ispatın aşamalarını ifade eden bir algoritmanın işleyişini algoritmik doğal dil ve akış şeması yardımıyla ifade ediniz.

Algoritmik Doğal Dil ile Artan Fonksiyon Kontrolü

1. Başla
2. Kullanıcıdan doğrusal bir fonksiyon al (f(x))

3. Artanlık kontrolü yap:

• i sayma sayısı için
• Eğer f(xᵢ₊₁) ≥ f(xᵢ) ise, f(x) artan fonksiyondur
• Değilse, f(x) artan fonksiyon değildir

4. Sonucu yazdır:

• Eğer eşitsizlik sağlanıyorsa: “f(x) artan fonksiyondur” yaz
• Aksi takdirde: “f(x) artan fonksiyon değildir” yaz

5. Bitir

4. Mantık Bağlaçları ve Niceleyiciler:

Bu ispatta ∀ (her) ve ⇒ (ise) bağlaçları kullanılmıştır. Tüm gerçek sayılar için bu fonksiyonun artan olduğunu ispatlamak amacıyla evrensel niceleyici (∀) kullanılır. Ayrıca f(x₁) < f(x₂) sonucunu göstermek için koşullu bağlaç (⇒) önemlidir.