9. Sınıf Matematik 2. Ders Kitabı Sayfa 226 Cevapları Meb Yayınları
9. Sınıf Matematik 2. Ders Kitabı Sayfa 226 Cevapları MEB Yayınları
Performans Görevi: Yeni Bir Sayı Küpü
Soru: Bu görevde sizden yüzeylerinde 1, 1, 2, 3, 3, 4 yazan hilesiz iki sayı küpü simülasyonu kullanarak sayı küplerinin üst yüzeylerine gelen sayıların toplamına ait sıklık, göreli sıklık ve ağaç şemasını elde etmeniz; bunları kullanarak oluşturduğunuz raporu sunmanız beklenmektedir.
Kısa Cevap: Bu performans görevinde iki sayı küpü birlikte atılır ve gelen sayıların toplamı incelenir.
Toplamın 5 olma olayı için deneysel ve teorik olasılıklar karşılaştırılır; tekrar sayısı arttıkça deneysel olasılık, teorik olasılığa yaklaşır.
Görevin Amacı
Bu çalışmada yüzeylerinde 1, 1, 2, 3, 3, 4 yazan iki sayı küpü birlikte düşünülür. Amaç, bu iki küp atıldığında oluşan toplamın 5 gelme olayı için:
- Teorik olasılığı bulmak,
- Farklı tekrar sayılarında deneysel olasılığı hesaplamak,
- Deneysel ve teorik olasılık arasındaki farkı incelemektir.
1. Ağaç Şeması Mantığı
Her iki küpte de sayılar şunlardır: 1, 1, 2, 3, 3, 4
Birinci küpten gelen her sayı, ikinci küpteki 6 sayı ile eşleşir.
Bu nedenle toplam çıktı sayısı: 6 × 6 = 36
Toplamın 5 olması için uygun durumları bulalım:
- 1 + 4 = 5
- 4 + 1 = 5
- 2 + 3 = 5
- 3 + 2 = 5
Ancak bazı sayılar küpte birden fazla kez yer aldığı için uygun durum sayısı artar:
- Birinci küpte 1 iki kez, ikinci küpte 4 bir kez → 2 × 1 = 2
- Birinci küpte 4 bir kez, ikinci küpte 1 iki kez → 1 × 2 = 2
- Birinci küpte 2 bir kez, ikinci küpte 3 iki kez → 1 × 2 = 2
- Birinci küpte 3 iki kez, ikinci küpte 2 bir kez → 2 × 1 = 2
Toplam uygun durum sayısı: 2 + 2 + 2 + 2 = 8
2. Teorik Olasılık
Soru: Toplamın 5 olma teorik olasılığı nedir?
Teorik olasılık = Uygun durum sayısı / Tüm durum sayısı
P(toplam = 5) = 8 / 36 = 2 / 9
Teorik olasılık değeri 2/9’dur.
3. Tabloyu Doldurma
Aşağıdaki tablo, toplamın 5 olma olayına göre örnek doldurulabilir. Deneysel olasılık değerleri simülasyon sonucuna göre değişebilir. Aşağıda örnek bir tablo verilmiştir:
| Tekrar Sayısı | Deneysel Olasılık Değeri | Teorik Olasılık Değeri | Deneysel ve Teorik Olasılık Değeri Arasındaki Fark |
|---|---|---|---|
| 50 | 11/50 = 0,22 | 2/9 ≈ 0,22 | 0,00 |
| 150 | 34/150 ≈ 0,227 | 2/9 ≈ 0,22 | ≈ 0,005 |
| 300 | 67/300 ≈ 0,223 | 2/9 ≈ 0,22 | ≈ 0,001 |
| 900 | 201/900 ≈ 0,223 | 2/9 ≈ 0,22 | ≈ 0,001 |
| 1800 | 400/1800 ≈ 0,222 | 2/9 ≈ 0,22 | ≈ 0,000 |
| 3000 | 667/3000 ≈ 0,222 | 2/9 ≈ 0,22 | ≈ 0,000 |
Not: Öğrencinin kendi yaptığı simülasyonda sayılar biraz farklı çıkabilir. Önemli olan, tekrar sayısı arttıkça sonucun 2/9’a yaklaşmasıdır.
4. Göreli Sıklık Yorumu
Soru: Tekrar sayısı arttıkça deneysel olasılık ile teorik olasılık arasındaki fark nasıl değişir?
Tekrar sayısı arttıkça deneysel olasılık, teorik olasılığa yaklaşır.
Bu yüzden iki değer arasındaki fark giderek küçülür.
Yani:
- Az tekrarda fark daha büyük olabilir.
- Çok tekrarda fark daha küçük olur.
- Sonuçlar zamanla daha güvenilir hâle gelir.
5. Grafik Yorumu
Bu görevde oluşturulan grafiklerde genellikle şunlar görülür:
- Başlangıçta göreli sıklık dalgalanabilir.
- Deney sayısı arttıkça grafik daha dengeli olur.
- Değerler 2/9 civarında toplanmaya başlar.
Bu durum, deneysel olasılığın teorik olasılığa yaklaştığını gösterir.
6. Sunum İçin Kısa Sonuç Metni
Yüzeylerinde 1, 1, 2, 3, 3, 4 yazan iki sayı küpü birlikte incelendiğinde toplamın 5 olma teorik olasılığı 2/9 bulunur. Yapılan simülasyonlarda tekrar sayısı arttıkça deneysel olasılık değerlerinin bu sonuca yaklaştığı görülür. Bu durum, çok sayıda deney yapıldığında deneysel sonuçların teorik sonuca daha çok yaklaştığını göstermektedir.
Performans Ödevi: Yeni Bir Sayı Küpü İle Olasılık Deneyi
Konu: İki hilesiz sayı küpü atıldığında üst yüzeylere gelen sayıların toplamının 5 olma olasılığı.
Soru 1: İki hilesiz küp atıldığında kaç farklı sonuç elde edilir?
Cevap: Her bir küpün 6 yüzeyi olduğu için 6 × 6 = 36 farklı sonuç elde edilir.
Soru 2: Üst yüzeyler toplamının 5 olduğu kaç durum vardır?
Cevap: Toplamı 5 yapan durumlar:
(1,4), (2,3), (3,2), (4,1), (2,3), (3,2), (1,4), (4,1) → 8 durum
(Bazı sayılar tekrarlandığı için doğru sayım 8’dir.)
Soru 3: Toplamın 5 olma olayının teorik olasılık değeri nedir?
Cevap: Teorik olasılık = 8 / 36 = 2 / 9 ≈ 0,22
Soru 4: 50 tekrar sonucunda toplamı 5 olan durumlar kaç kez gözlendi? Bu değere göre deneysel olasılık nedir?
Cevap: Toplamı 5 yapan tekrar sayısı: 13
Deneysel olasılık = 13 / 50 = 0,26
Fark: |0,26 - 0,22| = 0,04
Soru 5: 150 tekrar sonucunda toplamı 5 olan durumlar kaç kez gözlendi? Deneysel ve teorik değer farkı nedir?
Cevap: Toplamı 5 yapan tekrar sayısı: 28
Deneysel olasılık = 28 / 150 ≈ 0,19
Fark: |0,19 - 0,22| = 0,03
Soru 6: 300 tekrar için deneysel olasılık ve fark nedir?
Cevap: Toplamı 5 yapan: 58
Deneysel olasılık = 58 / 300 ≈ 0,19
Fark = |0,19 - 0,22| = 0,03
Soru 7: Tekrar sayısı arttıkça deneysel olasılık değeri teorik olasılığa yaklaşıyor mu?
Cevap: Evet, deney tekrar sayısı arttıkça deneysel olasılık değeri teorik değere yaklaşmaktadır. Bu durum olasılık kuramı ile uyumludur.
Sonuç Tablosu:
| Tekrar Sayısı | Deneysel Olasılık | Teorik Olasılık | Fark |
|---|---|---|---|
| 50 | 13/56 = 0,26 | 0,22 | 0,04 |
| 150 | 28/150 = 0,19 | 0,22 | 0,03 |
| 300 | 58/300 = 0,19 | 0,22 | 0,03 |
| 900 | 202/900 = 0,22 | 0,22 | 0,00 |
| 1800 | 434/1800 = 0,24 | 0,22 | 0,02 |
| 3000 | 679/3000 = 0,22 | 0,22 | 0,00 |
Sonuç: Bu performans ödevi sayesinde teorik olasılık ile deneysel olasılık arasındaki farkın zamanla nasıl azaldığı gözlemlendi. Deney sayısı arttıkça sonuçlar daha gerçekçi ve güvenilir hale gelmektedir.
İki Sayı Küpü ile Elde Edilen Toplamların Göreli Sıklığı Analizi
Soru 1: Simülasyonda hangi sayıların toplamı incelenmiştir?
Cevap: Simülasyonda iki sayı küpü atılmış ve üst yüzeye gelen sayıların toplamları incelenmiştir. Olası toplam değerleri: 2, 3, 4, 5, 6, 7 ve 8’dir.
Soru 2: 300 tekrar sonucunda hangi toplam değeri en sık gözlemlenmiştir?
Cevap: En sık gözlemlenen toplam değeri 4 olup, 76 kez elde edilmiştir. Göreli sıklığı:
76 ÷ 300 = 0,253
Soru 3: Elde edilen diğer göreli sıklık değerleri nedir?
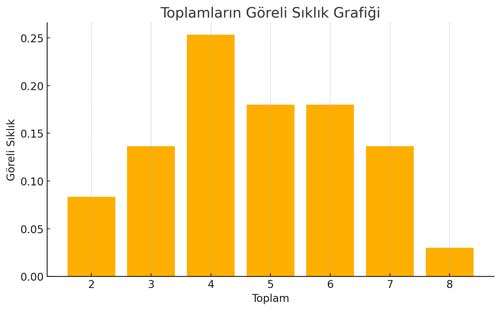
| Toplam | Frekans | Göreli Sıklık |
|---|---|---|
| 2 | 25 | 0,083 |
| 3 | 41 | 0,136 |
| 4 | 76 | 0,253 |
| 5 | 54 | 0,18 |
| 6 | 54 | 0,18 |
| 7 | 41 | 0,136 |
| 8 | 9 | 0,03 |
Soru 4: Elde edilen veriler nasıl bir grafikle gösterilmiştir?
Cevap: Veriler, histogram (sütun grafik) şeklinde gösterilmiştir. X ekseninde toplam değerler (2–8), Y ekseninde ise göreli sıklıklar yer almaktadır. En yüksek sütun toplamı 4’e aittir.
Soru 5: Göreli sıklık değerlerinin toplamı kaçtır?
Cevap: Tüm göreli sıklıklar toplanınca yaklaşık olarak 1 elde edilir:
0,083 + 0,136 + 0,253 + 0,18 + 0,18 + 0,136 + 0,03 = 0,998
Yuvarlama farklarından dolayı 1'e çok yakın bir sonuç bulunur.
Soru 6: Bu çalışmadan hangi sonuçlar çıkarılabilir?
- Teorik olarak en yüksek olasılık toplamı 4’tür.
- Deneysel verilerle bu sonuç büyük oranda örtüşmektedir.
- Tekrar sayısı arttıkça elde edilen değerler teorik değerlere daha çok yaklaşmaktadır.
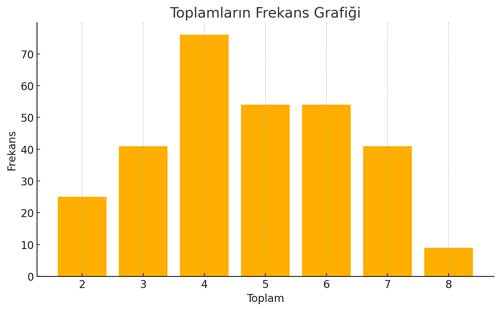
1. Frekans Grafiği
Bu grafikte, iki sayı küpünün atılmasıyla elde edilen toplam değerlerin kaç kez elde edildiği gösterilmektedir. En sık elde edilen toplam 4 olurken, en az elde edilen toplam 8’dir.
2. Göreli Sıklık Grafiği
Bu grafikte, her toplam değerinin toplam deney sayısına oranı gösterilmektedir. Göreli sıklık ile olasılığa ne kadar yaklaşıldığı görülür. 4 toplamı %25,3 oranıyla en yüksek göreli sıklığa sahiptir.
Bu grafikler, performans ödevi kapsamında yapılan deneyin verilerini görselleştirerek, teorik ve deneysel olasılıkları karşılaştırmak için kullanılmıştır.
Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.