9. Sınıf Matematik 1. Ders Kitabı 2. Tema/Ölçme ve Değerlendirme Cevapları Meb Yayınları

2. Tema/Ölçme ve Değerlendirme Cevapları

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 171

1. Soru: Yüksekliği 200 cm olan dik dairesel silindir şeklindeki boş bir su tankına su doldurulmaktadır. 1 dakika boyunca sabit hızla su doldurulduğunda tanktaki suyun yüksekliği 1 cm olmaktadır. Tanka su doldurulmaya başlandığı andan itibaren zamana (dk) bağlı olarak tanktaki suyun yüksekliğinin (cm) değişimini gösteren fonksiyon f olsun.

a) f fonksiyonunun tanım ve görüntü kümelerini bulunuz.
Cevap:
Tanım kümesi: [0, 200]
Görüntü kümesi: [0, 200]

b) f fonksiyonunun cebirsel temsilini bulunuz.
Cevap: f(x) = x

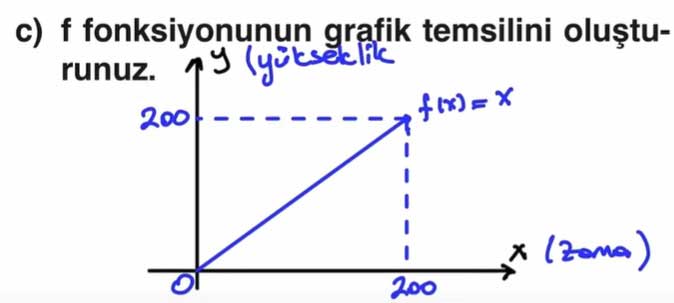
c) f fonksiyonunun grafik temsilini oluşturunuz.

ç) Tanımlı olduğu aralıkta f fonksiyonunun bire bir olup olmadığını bulunuz.
Cevap:
f(x) = x bire birdir.

d) f fonksiyonunun sıfırını ve işaretini belirleyiniz.
Cevap: Fonksiyonun sıfırı x=0 noktasında olur.
Fonksiyon, tanımlı olduğu [0,200] aralığında pozitiftir. Bu nedenle işareti pozitiftir.

2. Soru: Kenar uzunlukları 4 cm ve x cm olan bir dikdörtgen veriliyor. x≥1x olmak üzere (x e) cm bağlı olarak dikdörtgenin çevre uzunluğunun (cm) değişimini gösteren fonksiyon f olsun.

a) f fonksiyonunun tanım ve görüntü kümelerini bulunarak fonksiyonun cebirsel temsilini yazınız.
Cevap:

• Tanım Kümesi: [1, ∞)
• Görüntü Kümesi: [10, ∞)

Fonksiyonun cebirsel temsili:
f(x) = 2x + 8

Örnek hesaplama:
f(1) = 2 × 1 + 8 = 10

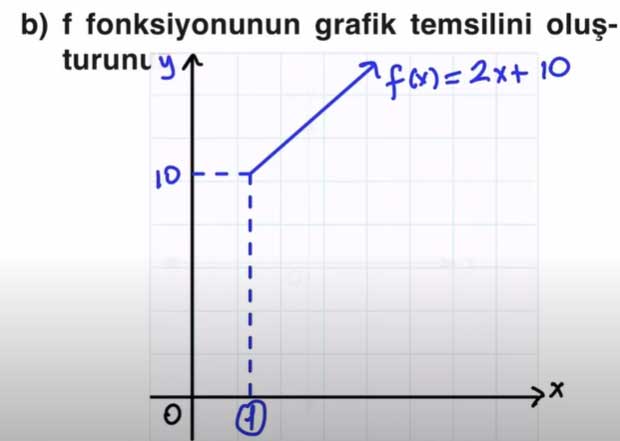
b) f fonksiyonunun grafik temsilini oluşturunuz.
Cevap: Fonksiyonun grafiği y = 2x + 10 doğrusu olacaktır.

c) f fonksiyonunun işaretini inceleyiniz.
Cevap: Fonksiyonun değerleri [1, ∞) aralığında pozitiftir.

ç) f fonksiyonunun artan veya azalan olduğu aralıkları belirleyiniz.
Cevap: [1, ∞) Fonksiyon, tanımlı olduğu tüm aralıkta artan bir fonksiyondur.

d) f fonksiyonunun bire bir olup olmadığını bulunuz.
Cevap: Fonksiyon bire birdir çünkü her x için yalnızca bir f(x) değeri vardır.

9. Sınıf Kimya Ders Kitabı Cevapları Meb Yayınları

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 172

Soru 3: Gerçek sayılarda tanımlı f fonksiyonunun grafiği aşağıda verilmiştir.
a) f fonksiyonunun cebirsel temsilini yazınız.
Cevap: Fonksiyonu f(x) = ax + b olarak alıyoruz.

• f(0) = 2 olduğuna göre:
  a * 0 + b = 2, buradan b = 2 bulunur.
• f(-1) = 0 olduğuna göre:
  -a + b = 0, buradan -a + 2 = 0 ve a = 2 bulunur.
  Sonuç: f(x) = 2x + 2.

b) f fonksiyonunun grafiğinin eğimini bulunuz.
Cevap: m = delta y / delta x = 2 / 1 = 2.

c) f fonksiyonunun sıfırını bulunuz.
Cevap: Fonksiyonun sıfırı, f(x) = 0 için:
2x + 2 = 0, buradan x = -1 bulunur.

ç) f fonksiyonunun işaretini bulunuz.
Cevap: Fonksiyonun işareti:

• x eleman (-∞, -1): f(x) < 0 (negatif).
• x eleman (-1, ∞): f(x) > 0 (pozitif).

Soru 4:
a) Barajın su depolama kapasitesinin en fazla kaç m³ olduğunu hesaplayınız.
Cevap: f(20) = 0 olduğuna göre:
-10000 * 20 + b = 0, buradan b = 200000 . 1000 = 200 000 000 bulunur.
En fazla kapasite: 200 000 000 m³.

b) Hangi yılın sonunda barajın su depolama kapasitesinin en az olduğunu bulunuz.
Cevap: Tabloya göre t = 20 yılında kapasite sıfır olur.

c) Barajın zamana bağlı su depolama kapasitesinin değişim oranını bulunuz.
Cevap: Değişim oranı: -10000 m³/yıl.

Soru 5:
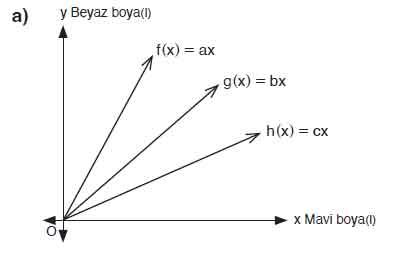
a) Verilen grafikleri hangi fonksiyonlara ait olduğunu bulunuz.
Cevap: Grafikte:

• f(x) = ax,
• g(x) = bx,
• h(x) = cx.

b) b katsayısının alacağı değeri bulunuz.
Cevap: b = 1 çünkü grafik üzerinde mavi ve beyaz renklerin eşit miktarda karıştırıldığı görülüyor. Bu, oranın bir birim fonksiyonuna (y = x) denk geldiğini gösterir.

c) a ve c katsayılarının alabileceği değerlerin aralıklarını bulunuz.
Cevap: Katsayı aralıkları:

• a > 1,
• 0 < c < 1.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 173

Soru 6: Aşağıdaki grafikte bir güneş enerji panelinin zamana (ay) bağlı enerji (kWh) üretim miktarı uygun aralıkta tanımlı f, g ve k doğrusal fonksiyonlarıyla ifade edilmiştir.

a) Hangi aylar arasında enerji üretim miktarının arttığını bulunuz.
Enerji üretimi 3. aydan 7. aya kadar artar.

b) Hangi aylar arasında enerji üretim miktarının azaldığını bulunuz.
Enerji üretimi 7. aydan 9. aya kadar azalır.

c) 7 ve 8. ay ile 8 ve 9. ay arasındaki enerji üretim miktarlarını karşılaştırınız.
7. ve 8. Ay ile 8. ve 9. Ay Arasındaki Enerji Üretim Miktarlarının Karşılaştırılması:

7. ve 8. Ay Arasında: Enerji üretim miktarı sabittir. Üretim 370 kWh olarak kalır, yani bir değişim gözlenmez.

8. ve 9. Ay Arasında: Enerji üretim miktarı artar. 370 kWh’den 420 kWh’ye yükselir, bu nedenle üretim 50 kWh artar.

Sonuç: 8. ve 9. ay arasındaki enerji üretimi, 7. ve 8. ay arasına göre daha hızlı bir değişim göstermektedir.

d) 3. aydan 9. aya kadar zamana (ay) bağlı enerji üretim miktarını (kWh) temsil eden parçalı gösterimli fonksiyonun cebirsel temsillerini ifade ediniz.
3. aydan 9. aya kadar enerji üretimini ifade eden parçalı fonksiyon şu şekilde tanımlanır:

f(x) =
75x - 5 , 3 ≤ x < 5
25x + 245 , 5 ≤ x < 7
-50x + 770 , 7 ≤ x < 8
-120x + 1330 , 8 ≤ x ≤ 9

Bu parçalı fonksiyon, her zaman aralığında enerji üretiminin değişimini ifade etmektedir. Her bir aralık için üretim miktarının doğrusal bir fonksiyonla temsil edildiği görülür.

Soru 7: Bir fabrikada yaklaşık 180 ml olarak dolum yapılan kutu sütlerin gerçek hacimlerinde belirli bir hata payı olabileceği öngörülmektedir. Bu hata payının en fazla 5 ml olduğu bilindiğinden bir kutu sütün gerçek hacminin [175, 185] ml olduğu ifade edilmektedir. Bir kutu sütün gerçek hacmine (ml) bağlı hata payını (ml) ifade eden fonksiyon f olsun.

a) f fonksiyonunun tanım ve görüntü kümelerini belirleyiniz.

Tanım ve görüntü kümeleri:

• Tanım kümesi: [175, 185]
• Görüntü kümesi: [0, 5]

b) f mutlak değer fonksiyonunu cebirsel olarak ifade ediniz.
Mutlak değer fonksiyonunun cebirsel ifadesi: f(x) = |x - 180|

c) f fonksiyonunun sıfırını bulup f fonksiyonunun parçalı gösterimini yazınız.
Fonksiyonun sıfırı ve parçalı gösterimi:
Fonksiyon sıfır olduğunda: f(x) = |x - 180| = 0 olduğundan x = 180.

Fonksiyonun parçalı gösterimi: f(x) =
180 - x, 175 ≤ x < 180
x - 180, 180 ≤ x ≤ 185

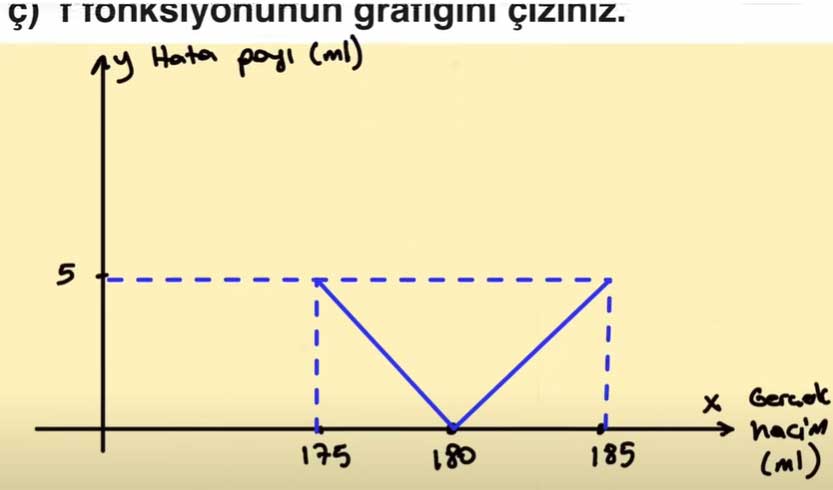
ç) f fonksiyonunun grafiğini çiziniz.

d) Fonksiyonun grafiği:

• Grafik x = 180 noktasında minimum (f(180) = 0) yapar.
• x = 175 ve x = 185 noktalarında f(x) = 5 olur.
• Grafik x = 180 noktasında simetrik bir V şekli oluşturur.

d) f fonksiyonunun bire bir olup olmadığını bulunuz.
Fonksiyonun bire bir olup olmadığının değerlendirilmesi:

• Fonksiyon bire bir değildir.
  Çünkü f(x) fonksiyonunun aynı görüntü değerini farklı x değerlerinde alır:
  Örneğin, f(175) = 5 ve f(185) = 5.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 174

8. Soru Görseldeki gibi aralarında 36 m bulunan Ayhan ve Bilge, saat 12:05’te aynı anda harekete başlayarak aynı yönde 24 dakika boyunca sabit hızla bisiklet sürmüştür. A noktasından harekete başlayan Ayhan dakikada 30 m, B noktasından harekete başlayan Bilge’nin dakikada 27 m yol aldığı bilinmektedir.

a) Ayhan ve Bilge’nin zamana bağlı aralarındaki mesafeyi modelleyen fonksiyonun farklı temsillerle gösteriniz.
Cebirsel temsili:
f(x) = 36 - 3x, 0 ≤ x ≤ 24

Grafik Temsili:

• Başlangıçta mesafe 36 m’dir.
• x = 12’de mesafe sıfıra iner (Ayhan ve Bilge buluşur).

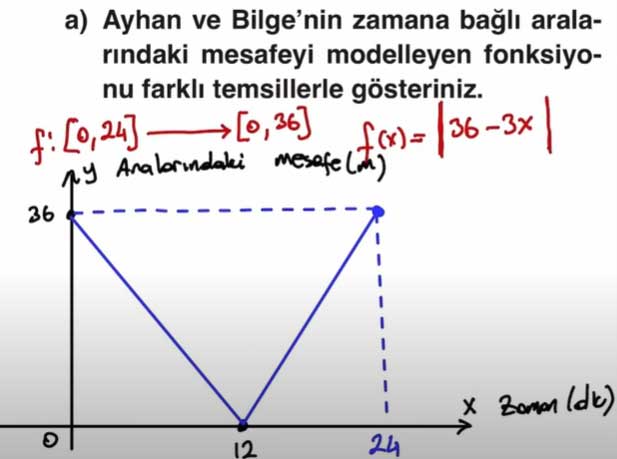
b) Fonksiyonun maksimum ve minimum değerlerini, fonksiyonun sıfırını belirleyerek problem bağlamındaki anlamını ifade ediniz.

• Maksimum değer: 36 (Başlangıçtaki mesafe).
• Minimum değer: 0 (Ayhan ve Bilge’nin buluştuğu an).
  Sıfırı 12'dir.

c) Ayhan ve Bilge’nin aralarındaki mesafe 12 metre olduğunda saatin kaç olduğunu bulunuz.

36 - 3x = 12

İlk çözüm:

• 36 - 3x = 12
• -3x = 12 - 36
• -3x = -24
• x = 8

İkinci çözüm:

• 36 - 3x = -12
• -3x = -12 - 36
• -3x = -48
• x = 16

Sonuç:

• İlk durumda x=8x = 8x=8, saat 12:13’ü gösterir.
• İkinci durumda x=16x = 16x=16, saat 12:21’i gösterir.

d) Ayhan ve Bilge’nin aralarındaki mesafenin 6 metreden ve 6 metreden daha fazla olduğu anlarda saatin gösterdiği değerlerin aralığını bulunuz.

Denklem şu şekilde çözülmüştür:

Denklem:

36 - 3x > 6

İlk çözüm:

• 36 - 3x > 6
• -3x > 6 - 36
• -3x > -30
• x < 10 (eşitsizlik yön değiştirir)

İkinci çözüm:

• 36 - 3x ≤ -6
• -3x ≤ -6 - 36
• -3x ≤ -42
• x ≥ 14 (eşitsizlik yön değiştirir)

Zaman Aralığı:

İlk aralık: 10 < x < 14

• 12.05 ile 12.15 arasında

İkinci aralık: x ≥ 14

• 12.19 ile 12.29 arasında

Sonuç: Ayhan ve Bilge’nin aralarındaki mesafenin 6 metre olduğu veya bu mesafeden daha fazla olduğu zaman dilimi:

• 12:05 - 12:15 ve 12:19 - 12:29 arasındadır.

9. Soru

Fonksiyonlar:

• g(x) = -3x + b1
• h(x) = -3x + b2
• k(x) = -3x + b3

Sıfır Noktalarının Hesaplanması:

g(x) = 0 için:

• -3x + b1 = 0
• x1 = b1 / 3

h(x) = 0 için:

• -3x + b2 = 0
• x2 = b2 / 3

k(x) = 0 için:

• -3x + b3 = 0
• x3 = b3 / 3

Sıralama: x2 < x1 < x3

Bu sıralamayı kullanarak:

• b2 / 3 < b1 / 3 < b3 / 3
• Buradan b2 < b1 < b3 sonucu elde edilir.

Sonuç

b2 < b1 < b3

10. Soru

Bir öğünde hastanın kolesterol kısıtlamasına uyumunu kontrol ediniz.

a) Eşitsizlik yazınız.
200 g et = 130 mg
320 - 130 = 190 mg
100 g tereyağı = 215 mg
1 g tereyağı = 2.15 mg
2.15x ≤ 190
x ≤ 88.37

b) 390 gram et ile tereyağı miktarını belirleyiniz.
390 g et = 253.5 mg
320 - 253.5 = 66.5 mg
66.5 / 2.15 = 30.93 g.
Tereyağı miktarı en fazla 30.93 g olmalıdır.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 175

11. Soru: Ekonomi ve Kumaş Üretimi

a) Kumaş üretimi için arz ve talebin dengede olduğu durumda kaç ton kumaş üretilmesi gerektiğini ve üretilen kumaş fiyatının kaç Türk lirası olması gerektiğini bulunuz.

Verilen denklem:
x/2 - 3 = 21 - x

Her iki tarafı düzenleyelim: x/2 + x = 24
Ortak paydayı dikkate alarak toplayalım: 3x/2 = 24
Her iki tarafı 2 ile çarpalım: 3x = 48
x’i bulmak için her iki tarafı 3’e bölelim: x = 16

Kumaş miktarı:
f(16) = 16/2 - 3 = 8 - 3 = 5 ton

16 . 50 000 = 800 000 TL

b) Arzı modelleyen f fonksiyonunun grafiği y ekseni boyunca pozitif yönde 3 birim ötelenildiğinde elde edilecek yeni denge noktasına göre kumaşın üretim miktarındaki ve 1 ton kumaşın fiyatındaki değişimi bulunuz.

Denklem:
f(x) = x/2 - 3 + 3
f(x) = x/2

1. x/2 - 3 = 21 - x denklemini düzenleyelim:
   x/2 + x = 21
   3x/2 = 42
   x = 14

2. Yeni denge noktasındaki kumaş üretim miktarını bulalım:
   f(14) = 14/2 = 7 ton

Kumaş üretim miktarındaki değişim:
7 - 5 = 2 ton artmış.

1 ton kumaş fiyatındaki değişim:
14 * 50.000 = 700.000 TL

1 ton maliyet hesabı:
1 ton maliyeti = 700.000 / 7 = 100.000 TL

Sonuç:

• Kumaş üretimi 2 ton artmıştır.
• 1 ton kumaş fiyatı 100.000 TL olmuştur.

12. Soru: Araç Kiralama ve Maliyet

a) x kilometre kullanılan bir aracın toplam kiralama maliyetini ifade eden fonksiyonları yazınız.

1. Şirket: f1(x) = 2000 + 3x
2. Şirket: f2(x) = 1500 + 5x

b) 1. ve 2. şirketin toplam kiralama maliyetini ifade eden fonksiyonların grafiklerini çizin.

Grafikler çizilmiştir. 1. Şirketin eğimi daha düşük olduğundan uzun mesafede daha avantajlıdır.

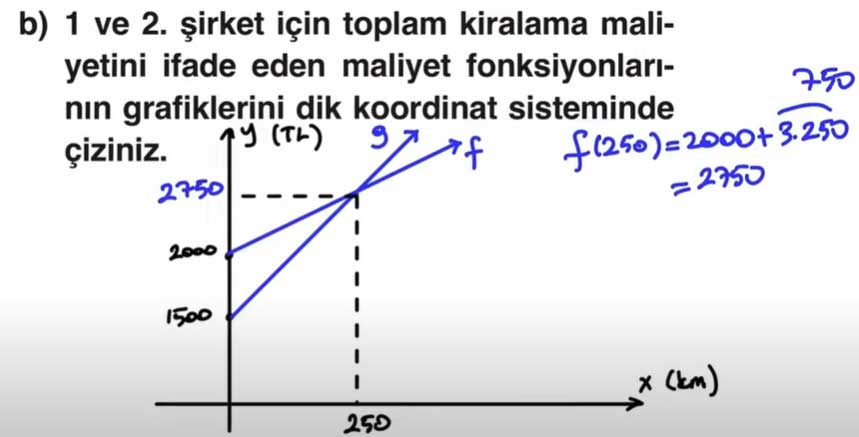
c) En az kaç kilometrelik kullanımda 1. şirketin maliyetinin 2. şirketin maliyetinden daha ekonomik olduğunu bulunuz.
f1(x) < f2(x)
2000 + 3x < 1500 + 5x
500 < 2x
x > 250

En az 251 kilometrede 1. şirket daha ekonomiktir.

13. Soru: Tatil Bütçesi ve Gece Sayısı

Sorular:

a) Orhan Bey'in bütçesini aşmayacak şekilde tatil planı ifade eden eşitsizliği oluşturunuz.

Tatildeki toplam harcama: 8000x + 2000 ≤ 35000

b) Orhan Bey'in bütçesi aşılmadan en fazla kaç gece kalabileceğini bulunuz.
8000x ≤ 33000
x ≤ 33000 / 8000
x ≤ 4

Orhan Bey en fazla 4 gece konaklayabilir.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 176

14. Bir kırtasiye, fotokopi makinesi kiralayacaktır. 2 tane fotokopi makinesi, istediği ölçütlere uygundur. Bu makinelerin çalışma süresine (dk.) bağlı olarak elektrik maliyeti ve sabit depozito bedeli (TL) bilgileri Tablo 1’de verilmiştir.

a) A ve B makinelerinin çalışma süresine (dk.) bağlı toplam maliyetlerini (TL) ifade eden fonksiyonlar:

A makinesi için: f(x) = 5000 + 0,25x
B makinesi için: g(x) = 4000 + 0,65x

b) Fonksiyonlar kullanılarak verilen çalışma süreleri için toplam maliyetler:

A makinesi için:
f(1000) = 5000 + 0,25 * 1000 = 5250
f(1500) = 5000 + 0,25 * 1500 = 5375
f(2000) = 5000 + 0,25 * 2000 = 5500
f(2500) = 5000 + 0,25 * 2500 = 5625
f(3000) = 5000 + 0,25 * 3000 = 5750

B makinesi için:
g(1000) = 4000 + 0,65 * 1000 = 4650
g(1500) = 4000 + 0,65 * 1500 = 4875
g(2000) = 4000 + 0,65 * 2000 = 5300
g(2500) = 4000 + 0,65 * 2500 = 5625
g(3000) = 4000 + 0,65 * 3000 = 5850

c) A ve B makinelerine ait toplam maliyet fonksiyonlarının grafiklerini dik koordinat
sisteminde çiziniz.

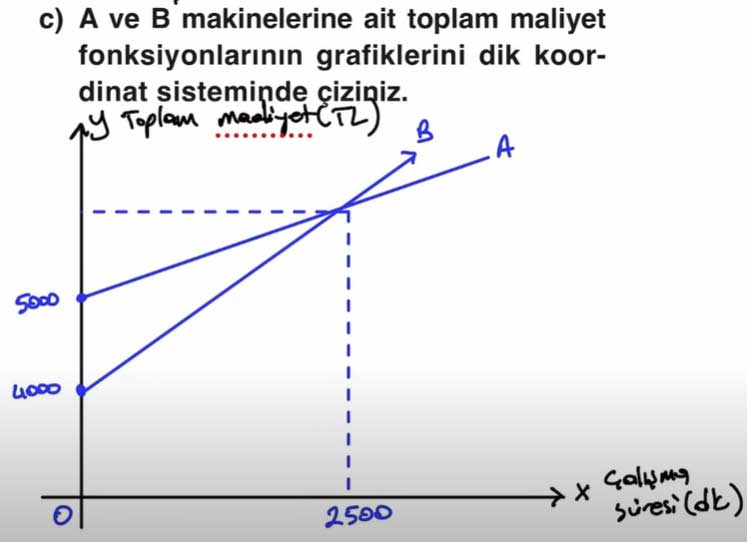
ç) A ve B makinelerinin toplam maliyetlerinin kaç dakikalık çalışma süresi sonunda
ve kaç Türk lirasında eşitleneceğini grafik gösteriminden yararlanarak bulunuz.

f(x) = g(x)
5000 + 0,25x = 4000 + 0,65x
1000 = 0,40x
x = 2500

Kesişim noktası: (2500, 5625)

Grafik incelendiğinde, A ve B makinelerinin toplam maliyet fonksiyonları x = 2500 dakikada kesişmektedir.
Bu noktada toplam maliyet:
f(2500) = g(2500) = 5625 TL

Sonuç: Toplam maliyetler, 2500 dakikalık çalışma süresi sonunda 5625 TL olarak eşitlenir.

d) A ve B makinelerinin toplam maliyetlerinin kaç dakikalık çalışma süresi sonunda
eşitleneceğini cebirsel çözüm yaparak bulunuz.

Yukarıdaki hesaplamalar sonucunda maliyetlerin x = 2500 dakikada eşitlendiği doğrulanmıştır.

Fonksiyonlar:
A makinesi: f(x) = 5000 + 0,25x
B makinesi: g(x) = 4000 + 0,65x

Eşitlik durumu:
f(x) = g(x)
5000 + 0,25x = 4000 + 0,65x
1000 = 0,40x
x = 2500

Sonuç: Toplam maliyetler 2500 dakikada eşitlenir.

e) A ve B makinelerine ait 1000, 1500, 2000, 2500 ve 3000 dakikalık çalışma süresi sonundaki toplam maliyetleri karşılaştırarak hangi makinenin daha ekonomik olduğunu belirleyiniz.

x ≤ 2500 dakikaya kadar B makinesi daha ekonomiktir.
x > 2500 dakikadan sonra A makinesi daha ekonomiktir.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 177

15. Aşağıdaki görselde su sebilleri üzerinde duran dik dairesel silindir kaplar verilmiştir.

a) I ve II numaralı kaplara ait zamana (dk.) bağlı su yüksekliğini ifade eden fonksiyonun cebirsel temsilini yazınız.

• I. Damacana (Tablo 1):
  Başlangıç yüksekliği: 40 cm
  Azalma oranı: 4 cm/dk
  Fonksiyon: f₁(x) = 40 - 4x

• II. Damacana (Tablo 2):
  Başlangıç yüksekliği: 30 cm
  Azalma oranı: 2 cm/dk
  Fonksiyon: f₂(x) = 30 - 2x

b) Cebirsel temsilini yazdığınız fonksiyonların grafiklerini çiziniz.

• I. Damacana için: f₁(x) = 40 - 4x
  Başlangıçta y-eksenini 40'tan keser ve eğim -4'tür.

• II. Damacana için: f₂(x) = 30 - 2x
  Başlangıçta y-eksenini 30'dan keser ve eğim -2'dir.

c) Hangi kaptaki suyun daha çabuk tükeneceğini bulunuz.

I. Damacana (f₁(x)):
40 - 4x = 0
x = 10 dakika

II. Damacana (f₂(x)):
30 - 2x = 0
x = 15 dakika

Sonuç: I. Damacana suyu daha çabuk tükenir.

ç) Kaplardaki suların yüksekliklerinin kaçıncı dakikada eşit olduğunu bulunuz.

Eşitlik durumu:
f₁(x) = f₂(x)
40 - 4x = 30 - 2x
10 = 2x
x = 5 dakika

Sonuç: Kaplardaki su yükseklikleri 5. dakikada eşittir.

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 178

16. Soru: Buna göre zamana (dk.) bağlı olarak bandın başlangıcından pistin diğer ucuna kadar bu kayakçıların aldıkları mesafeyi (m) gösteren fonksiyonların grafik temsilleri aşağıdakilerden hangisi olabilir?

Yorum ve Çözüm:

• g fonksiyonu: İki kat hızda hareket eden 2. kayakçı, en hızlı varır.
• n fonksiyonu: Duran ve sonra hareket eden 3. kayakçı, orta hızla hareket eder.
• f fonksiyonu: Sabit hızda hareket eden 1. kayakçı, en geç varır.

Doğru Grafik Seçimi: B

17. Soru:İç mekânları belirli sıcaklık, nem ve hava kalitesi seviyelerine getirme işlemine iklimlendirme denir. İklimlendirilen bir odada yapılan hava sıcaklığı ölçümlerinde zamana (sa.) bağlı sıcaklık (^oC) değerlerindeki değişimi gösteren, uygun aralıkta tanımlı f ve g fonksiyonlarının grafikleri aşağıda verilmiştir.

Yorum ve Çözüm:

1. f(x) grafiği: Hava sıcaklığı, başlangıçta sabit 0°C'dir ve 2. saatten itibaren artmaya başlar.
2. g(x) grafiği: Hava sıcaklığı, 2. saatten sonra 8°C azalır.

Seçeneklerin Kontrolü:

• A) 7 saat boyunca 0°C altında değil, Yanlış.
• B) 18 saat boyunca 0°C’nin üzerinde değil, Yanlış.
• C) Hava sıcaklığı 10 saat azalmış, Doğru.
• D) 12 saat boyunca artmamış, Yanlış.
• E) İlk ve son sıcaklık farkı 4°C değil, Yanlış.

Doğru Cevap: C

9. Sınıf Matematik Ders Kitabı Cevapları Meb Yayınları (1. Kitap) Sayfa 179

18. Soru: Görselde verilen haritada doğrusal bir yol üzerinde gerçek sayı doğrusu modellenmiştir. Sayı doğrusu üzerinde Can’ın evinin konumu O noktasıyla,
kütüphane ve marketin konumları sırasıyla K(-5) ve M(3) noktalarıyla gösterilmiştir

Fonksiyon Değerleri:

• f(i) = (-5, 3) → [0, 500]
• f(x) = 100x

Fonksiyon tanımlanarak: (-5) + 3 - 0 - 0 + 500 / 100 = 3

Doğru Cevap: 3 (D şıkkı)

Fonksiyon tanımı: f : (a, b) → [c, d], f(x) = |kx + n|

Değerler:

• a = -5
• b = 3
• c = 0
• d = 500

Çözüm:

Fonksiyon parametrelerinin belirlenmesi:

• f(x) = |kx + n|
• x = -5 için f(x) = |k(-5) + n| = 0 ⇒ n = 0
• x = -5 ve f(x) = 500 ⇒ |-5k| = 500 ⇒ k = 100

İfade hesaplama:

• a + b - c - n + d / k
• -5 + 3 - 0 - 0 + 500 / 100
• -5 + 3 + 5 = 3

Sonuç: Doğru cevap: D) 3

19. Soru:Fadime Hanım, evden ofisine doğru sabit hızla yürümeye başlamıştır. Fadime Hanım’ın telefonunu evde unuttuğunu fark eden kızı Derya da bir süre sonra evden çıkmış ve sabit hızla annesi ile aynı yoldan ilerlemeye başlayarak annesi ofise varmadan ona yetişmiştir. Aynı noktadan harekete başlayan Fadime Hanım ve Derya’nın zamana (dk.) bağlı aldıkları mesafeyi (m) gösteren fonksiyonlar sırasıyla f ve d fonksiyonları olsun. Uygun aralıkta tanımlı f ve d fonksiyonlarının cebirsel temsilleri f(t) = 70t ve d(t) = 90t - 360 biçimindedir.

Verilenler:

1. f(t) = 70t
2. g(t) = 90t - 360

Analiz:

• I. İfade: 80t - 360 = 0, çözüm: t = 360 / 80 = 4 dakika Doğru.
• II. İfade: Fatma ve Derya arasında 1260 metre fark vardır. d(18) = 80 × 18 - 360 = 1260. Doğru.
• III. İfade: Fatma ve Derya arasındaki fark 12 dakika değildir. Yanlış.

Sonuç: Doğru ifadeler: I ve II (C şıkkı).